à NGHÄĻA CÃC Háŧ Sáŧ RÂē, fÂē, QÂē, qÂē TRONG Mà HÃNH PLS SEM
1. Háŧ sáŧ xÃĄc Äáŧnh RÂē hay RÂēhiáŧu
cháŧnh
RÂē hay RÂēhiáŧu
cháŧnh là cÃĄc háŧ sáŧ xÃĄc Äáŧnh máŧĐc Äáŧ giášĢi thÃch cáŧ§a biášŋn náŧi sinh trong
mÃī hÃŽnh SEM báŧi cÃĄc biášŋn ngoᚥi sinh liÊn quan Äášŋn nÃģ. Và dáŧĨ:
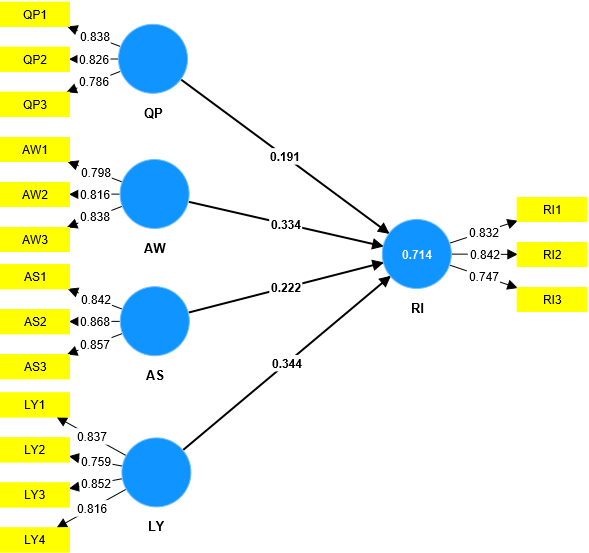
RÂē trong mÃī hÃŽnh trÊn là 71.4%, Äiáŧu
nà y nghÄĐa là 71.4% sáŧą biášŋn thiÊn cáŧ§a biášŋn RI ÄÆ°áŧĢc Äiáŧu cháŧnh báŧi 4 biášŋn Äáŧc lášp
trong mÃī hÃŽnh (QP, AW, AS, LY). Phᚧn trÄm sáŧą thay Äáŧi cáŧ§a biášŋn RI ÄÆ°áŧĢc Äiáŧu cháŧnh
báŧi cÃĄc yášŋu táŧ khÃĄc khÃīng cÃģ trong mÃī hÃŽnh nghiÊn cáŧĐu. Máŧt mÃī hÃŽnh nghiÊn cáŧĐu ÄÆ°áŧĢc
xem là Äᚥt yÊu cᚧu khi cÃģ RÂē láŧn (Äáŧi váŧi mÃī hÃŽnh háŧi qui báŧi thÃŽ RÂē lášĨy chuášĐn lÃ
âĨ 50%).
VÃ Äáŧ xem xÃĐt ÄÃĄnh giÃĄ máŧĐc Äáŧ giášĢi
thÃch cáŧ§a cÃĄc biášŋn ngoᚥi sinh táŧi biášŋn náŧi sinh trong mÃī hÃŽnh thÃŽ ngÆ°áŧi ta sáŧ dáŧĨng
háŧ sáŧ fÂē.
2. Háŧ sáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ giášĢi thÃch
cáŧ§a biášŋn ngoᚥi sinh táŧi biášŋn náŧi sinh fÂē
Háŧ sáŧ fÂē thÆ°áŧng ÄÆ°áŧĢc xem xÃĐt
cÃđng váŧi háŧ sáŧ xÃĄc Äáŧnh RÂē hiáŧu cháŧnh Äáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ giášĢi thÃch cáŧ§a cÃĄc biášŋn
ngoᚥi sinh táŧi biášŋn náŧi sinh trong mÃī hÃŽnh. Viáŧc ÄÃĄnh giÃĄ nà y nhášąm xem xÃĐt vai
trÃē giášĢi thÃch cáŧ§a biášŋn ngoᚥi sinh lÊn biášŋn náŧi sinh là cÃģ hay khÃīng? Và nášŋu cÃģ
thÃŽ máŧĐc Äáŧ là thášĨp hay cao? ThÃīng thÆ°áŧng, ngÆ°áŧi ta hay sáŧ dáŧĨng cháŧ sáŧ fÂē
Äáŧ xem xÃĐt láŧąa cháŧn cÃĄc biášŋn cÃģ máŧĐc Äáŧ giášĢi thÃch cao Äáŧ tášp trung nguáŧn láŧąc cášĢi
thiáŧn cÃĄc yášŋu táŧ nà y trong mÃī hÃŽnh nghiÊn cáŧĐu.
|
ÄÃĄnh giÃĄ máŧĐc Äáŧ giášĢi
thÃch cáŧ§a biášŋn ngoᚥi sinh lÊn biášŋn náŧi sinh bášąng háŧ sáŧ fÂē |
|
|
fÂē < 0.02 |
KhÃīng ÄÃģng vai trÃē giášĢi
thÃch |
|
0.02 âĪ f2 < 0.15 |
CÃģ máŧĐc giášĢi thÃch thášĨp |
|
0.15 âĪ f2 < 0.35 |
CÃģ máŧĐc giášĢi thÃch trung
bÃŽnh |
|
f2 âĨ 0.35 |
CÃģ máŧĐc giášĢi thÃch cao |
(Nguáŧn: Hair và cáŧng sáŧą, 2022)
Trong cÃĄc mÃī hÃŽnh háŧi qui báŧi thÃīng
thÆ°áŧng, chÚng ta sáŧ dáŧĨng SPSS Äáŧ phÃĒn tÃch và Ãt cÃģ ngÆ°áŧi nà o Äáŧ cášp táŧi háŧ sáŧ fÂē,
mà cháŧ tášp trung và o háŧ sáŧ háŧi qui trong mÃī hÃŽnh. NgÆ°áŧi ta hay dáŧąa và o háŧ sáŧ háŧi
qui (beta) Äáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ ášĢnh hÆ°áŧng cáŧ§a cÃĄc biášŋn Äáŧc lášp lÊn biášŋn pháŧĨ thuáŧc.
Và táŧŦ ÄÃģ là m cÆĄ sáŧ Äáŧ láŧąa cháŧn cÃĄc yášŋu táŧ cᚧn tášp trung nguáŧn láŧąc Äáŧ cášĢi thiáŧn
trong mÃī hÃŽnh nghiÊn cáŧĐu. Tuy nhiÊn viáŧc nà y cᚧn ÄÆ°áŧĢc xem xÃĐt thášt káŧđ, báŧi láš― váŧi
máŧt máŧi quan háŧ nhÃĒn quášĢ trong mÃī hÃŽnh cÃģ háŧ sáŧ háŧi qui cao thÃŽ chÆ°a hášģn háŧ sáŧ fÂē
cao. ChÚng ta hÃĢy cÃđng so sÃĄnh kášŋt quášĢ phÃĒn tÃch ÄÆ°áŧĢc táŧŦ mÃī hÃŽnh tháŧąc tášŋ trong
bášĢng dÆ°áŧi ÄÃĒy.
|
|
Háŧ sáŧ háŧi qui (beta) |
Háŧ sáŧ fÂē |
|
AS â RI |
0.222 |
0.110 |
|
AW â RI |
0.334 |
0.273 |
|
LY â RI |
0.344 |
0.264 |
|
QP â RI |
0.191 |
0.088 |
Äáŧ dáŧ
hÃŽnh dung, chÚng ta hÃĢy tráŧąc
quan hÃģa bášąng Äáŧ tháŧ nhÆ° sau:
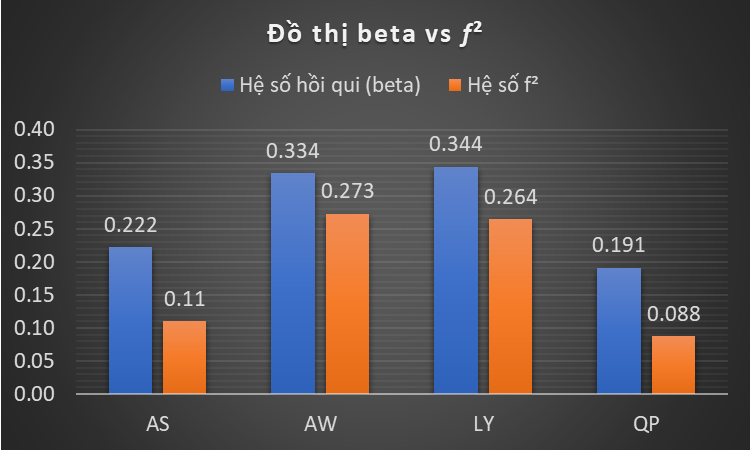
ChÚng ta cÃģ tháŧ thášĨy rášąng, tháŧĐ táŧą táŧŦ
láŧn táŧi bÃĐ cáŧ§a cÃĄc biášŋn Äáŧc lášp trong mÃī hÃŽnh theo háŧ sáŧ háŧi qui beta là LY, AW,
AS, QP. Tuy nhiÊn tháŧĐ táŧą táŧŦ láŧn táŧi bÃĐ theo háŧ sáŧ fÂē sáš― là AW, LY, AS,
QP. NÊn nášŋu nguáŧn láŧąc cáŧ§a máŧt doanh nghiáŧp cÃģ hᚥn, và bášŊt buáŧc cháŧ cháŧn máŧt yášŋu
táŧ táŧt nhášĨt Äáŧ cášĢi thiáŧn thÃŽ lÚc ÄÃģ chÚng ta nÊn cÃĒn nhášŊc thášt káŧđ.
3. Háŧ sáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ
dáŧą bÃĄo Q2
Q2 là máŧt cháŧ sáŧ cáŧ§a nÄng
láŧąc dáŧą bÃĄo ngoà i mášŦu (out-of sample predictive power) trong
mÃī hÃŽnh. Äáŧ tÃnh toÃĄn háŧ sáŧ Q2 nà y, trong phᚧn máŧm SmartPLS 4 cÃĄc bᚥn
cháŧn Calculate, nhášĨn cháŧn Blindfolding, tášĨt cášĢ cáŧĐ Äáŧ máš·c Äáŧnh và nhášĨn Start
calculation.

Äáŧc kášŋt quášĢ, chÚng ta click chuáŧt
và o máŧĨc Construct cross-validated redundancy. LÆ°u Ã― rášąng, háŧ sáŧ Q2 ÄÆ°áŧĢc
SmartPLS tÃnh toÃĄn bášąng 2 phÆ°ÆĄng phÃĄp khÃĄc nhau. Máŧt là phÆ°ÆĄng phÃĄp tiášŋp cášn phᚧn
dÆ° háŧ sáŧ chÃĐo (cross-validated redundancy), và hai là phÆ°ÆĄng phÃĄp tiášŋp cášn phᚧn
chung háŧ sáŧ chÃĐo (cross-validated communality). Cho nÊn, mà n hÃŽnh bÃĄo cÃĄo kášŋt
quášĢ sáš― xuášĨt hiáŧn táŧi 2 kášŋt quášĢ tÆ°ÆĄng áŧĐng váŧi 2 phÆ°ÆĄng phÃĄp tiášŋp cášn áŧ trÊn.
ChÚng ta sáŧ dáŧĨng kášŋt quášĢ nà o cÅĐng ok. Tuy nhiÊn, theo nhiáŧu tà i liáŧu khuyÊn rášąng,
phÆ°ÆĄng phÃĄp tiášŋp cášn phᚧn dÆ° háŧ sáŧ chÃĐo (cross-validated redundancy) cho kášŋt quášĢ
táŧt hÆĄn. VÃŽ vášy, chÚng tÃīi cÅĐng khuyÊn cÃĄc bᚥn sáŧ dáŧĨng kášŋt quášĢ táŧŦ phÆ°ÆĄng phÃĄp
tiášŋp cášn nà y.
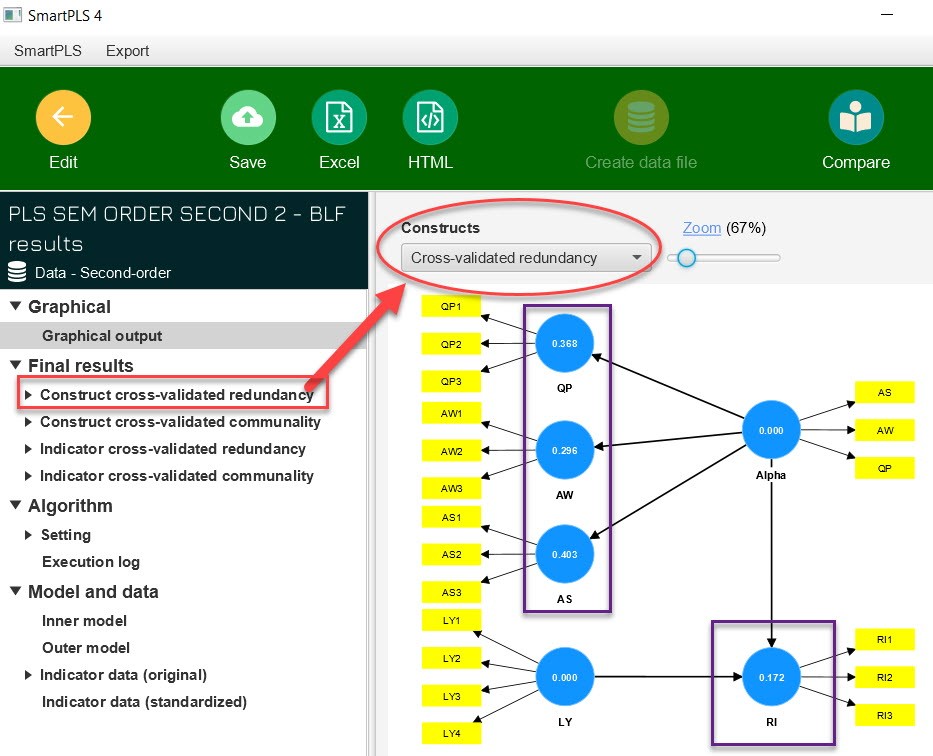
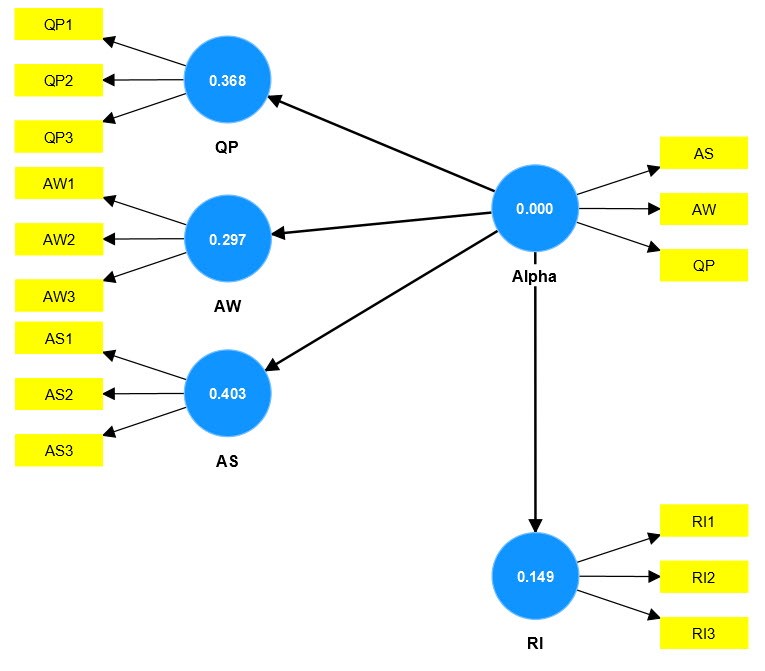
áŧ khung bÊn phášĢi mà n hÃŽnh, chÚng ta
thášĨy mÃī hÃŽnh cÃģ cÃĄc háŧ sáŧ Q2 nášąm bÊn trong cÃĄc vÃēng trÃēn (cÃĄc biášŋn
construct) tÆ°ÆĄng áŧĐng váŧi phÆ°ÆĄng phÃĄp tiášŋp cášn, chÚng ta cÃģ tháŧ cháŧn phÆ°ÆĄng phÃĄp
tiášŋp cášn Äáŧ mÃī hÃŽnh tháŧ hiáŧn háŧ sáŧ Q2 tÆ°ÆĄng áŧĐng. Máŧt Äiáŧu lÆ°u Ã― náŧŊa
rášąng, háŧ sáŧ Q2 cháŧ xuášĨt hiáŧn váŧi cÃĄc biášŋn náŧi sinh, váŧi cÃĄc biášŋn thuᚧn
ngoᚥi sinh sáš― khÃīng xuášĨt hiáŧn háŧ sáŧ Q2.
Kášŋt quášĢ áŧ và dáŧĨ phÃĒn tÃch trong
hÃŽnh: yášŋu táŧ RI cÃģ Q2 = 0.172, nghÄĐa là máŧĐc Äáŧ chÃnh xÃĄc váŧ dáŧą bÃĄo cáŧ§a
cášĨu trÚc RI (nÄng láŧąc dáŧą bÃĄo ngoà i mášŦu) là 17.2% âĪ 25%, nÊn theo
|
ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh
xÃĄc váŧ dáŧą bÃĄo |
|
|
0 < Q2 âĪ
0.25 |
ThášĨp |
|
0.25 < Q2
âĪ 0.5 |
Trung bÃŽnh |
|
Q2 > 0.5 |
Cao |
TrÊn ÄÃĒy là cÃĄch ÄÃĄnh giÃĄ máŧĐc Äáŧ váŧ
dáŧą bÃĄo theo háŧ sáŧ Q2 trÆ°áŧc giáŧ cÃĄc nghiÊn cáŧĐu hay dÃđng. Tuy nhiÊn,
theo
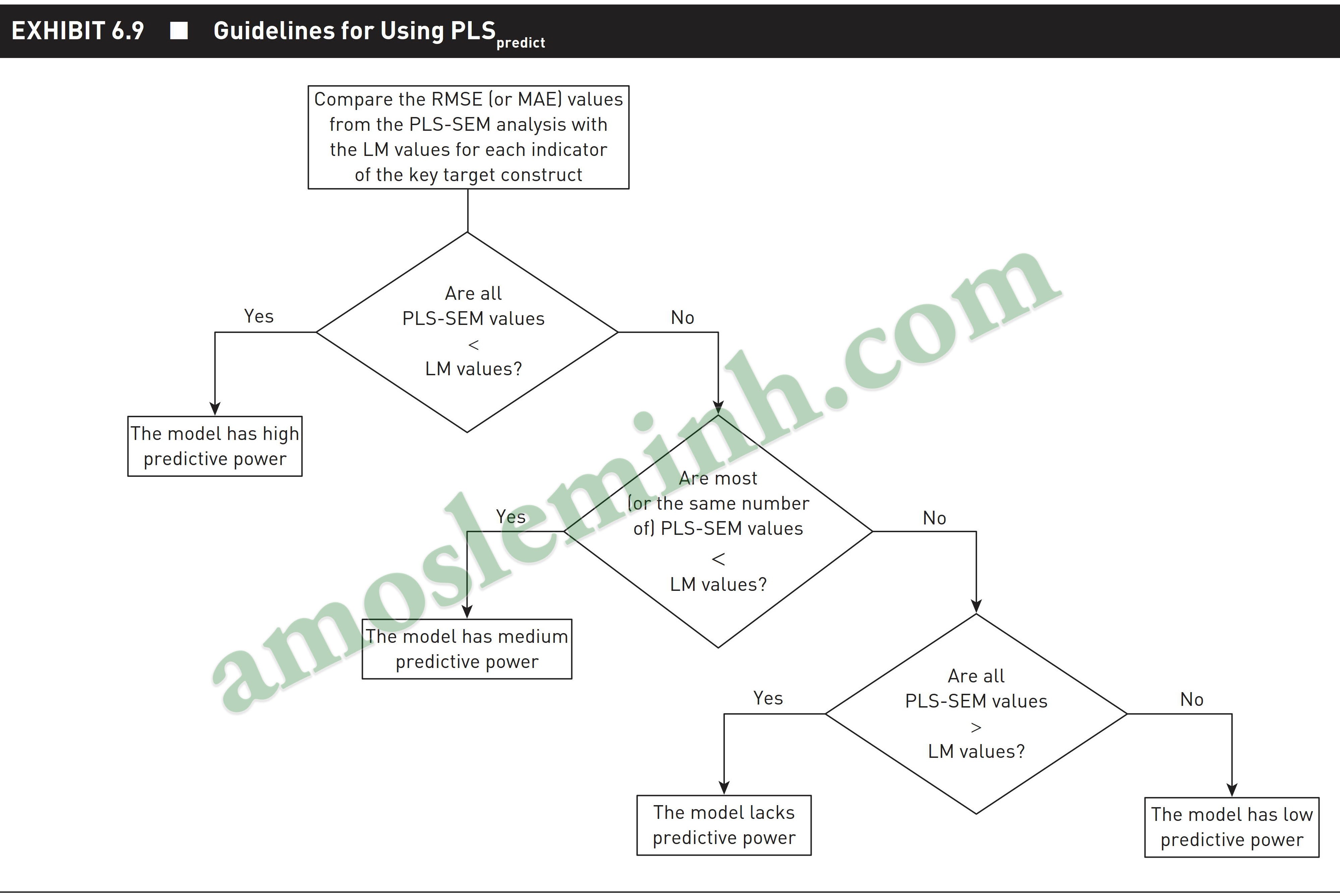
Tiášŋp theo, chÚng tÃīi sáš― hÆ°áŧng dášŦn
cÃĄc bᚥn cÃĄch tháŧĐc ÄÃĄnh giÃĄ máŧĐc Äáŧ dáŧą bÃĄo cáŧ§a mÃī hÃŽnh bášąng tháŧ§ táŧĨc PLSpredict
trong SmartPLS 4.
BÆ°áŧc 1:
Cháŧn tháŧ§ táŧĨc PLSpredict. Äáŧ máš·c Äáŧnh và chᚥy phÃĒn tÃch.
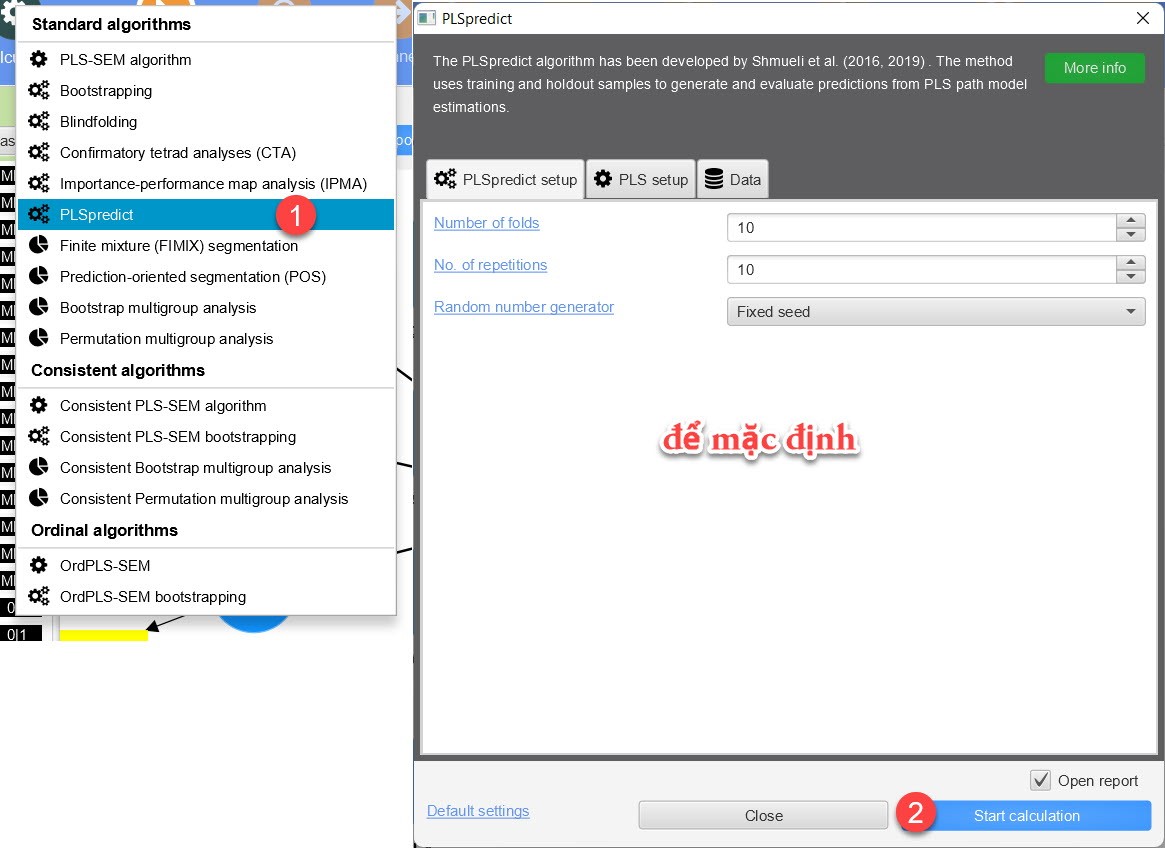
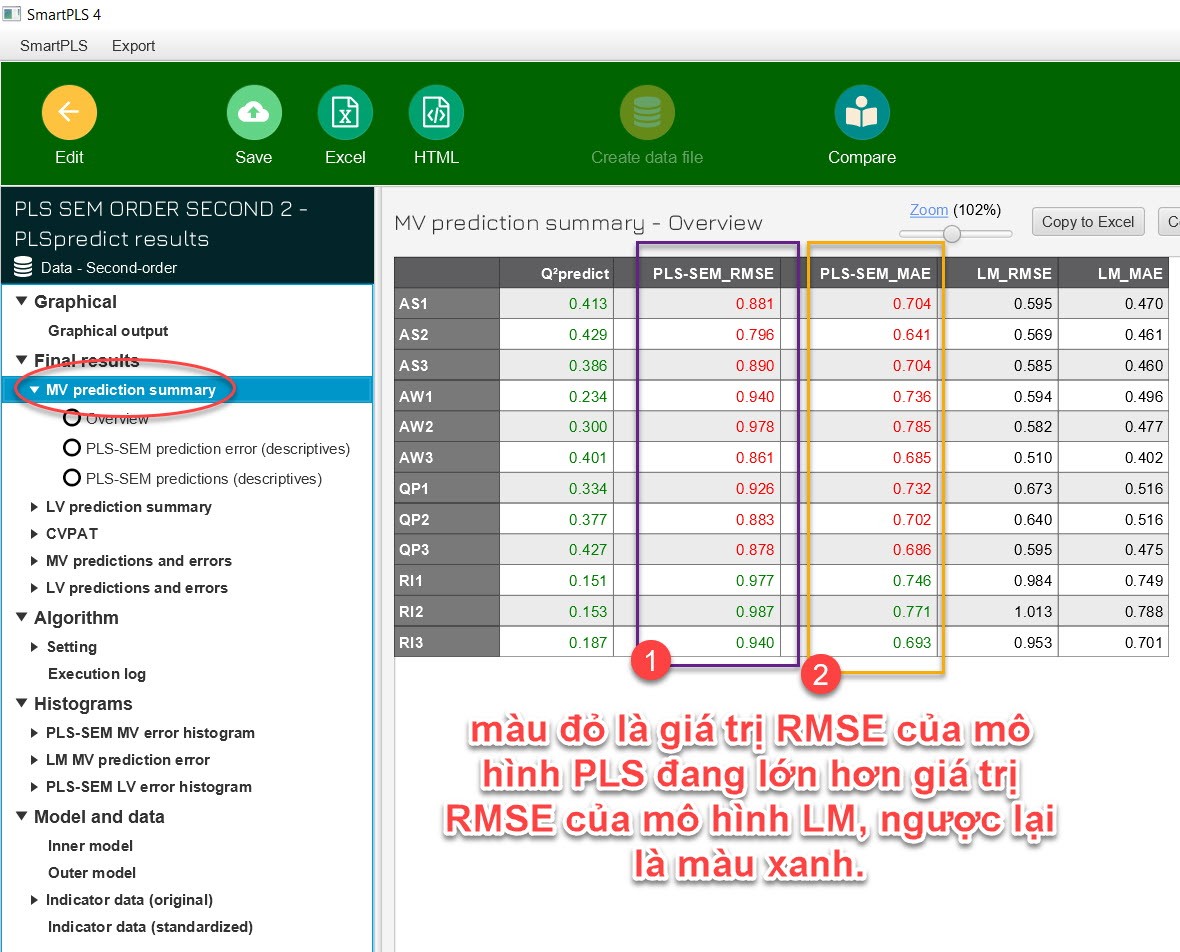
BÆ°áŧc 2:
Äáŧc kášŋt quášĢ. Bᚥn cháŧn máŧĨc MV prediction summary. Bᚥn cÃģ tháŧ sáŧ dáŧĨng cáŧt sáŧ 1
(RMSE) hoáš·c cáŧt sáŧ 2 (MAE) Äáŧu ÄÆ°áŧĢc. Kášŋt háŧĢp váŧi BášĢng Exhibit 6.9 cáŧ§a Hair và cáŧng
sáŧą (2022) Äáŧ kášŋt luášn váŧ nÄng láŧąc dáŧą bÃĄo cáŧ§a mÃī hÃŽnh. Kášŋt quášĢ và dáŧĨ cho thášĨy,
nÄng láŧąc dáŧą bÃĄo cáŧ§a mÃī hÃŽnh RI cao, cÃĄc mÃī hÃŽnh cÃēn lᚥi khÃīng cÃģ nÄng láŧąc dáŧą
bÃĄo.
4. Háŧ sáŧ ÄÃĄnh giÃĄ hiáŧu quášĢ dáŧą bÃĄo cáŧ§a
máŧt biášŋn giášĢi thÃch q2
Háŧ
sáŧ nà y ÄÆ°áŧĢc sáŧ dáŧĨng khi cÃĄc bᚥn ÄÃĄnh giÃĄ nÄng láŧąc dáŧą bÃĄo cáŧ§a mÃī hÃŽnh bášąng háŧ sáŧ
QÂē. Trong trÆ°áŧng háŧĢp cÃĄc bᚥn ÄÃĄnh giÃĄ nÄng láŧąc dáŧą bÃĄo cáŧ§a mÃī hÃŽnh bášąng tháŧ§ táŧĨc
PLSpredict thÃŽ khÃīng cᚧn ÄÃĄnh giÃĄ háŧ sáŧ q2, chÚng ta cháŧ
cᚧn ÄÃĄnh giÃĄ R2 và f2 là ÄÆ°áŧĢc (tham khášĢo Hair và cáŧng
sáŧą, 2022).
Háŧ
sáŧ ÄÃĄnh giÃĄ hiáŧu quášĢ dáŧą bÃĄo cáŧ§a máŧt biášŋn giášĢi thÃch q2 hay cÃēn gáŧi
là háŧ sáŧ tÃĄc Äáŧng q2. Q2 cáŧ§a biášŋn RI là 0.172 âĪ 0.25 â máŧĐc
Äáŧ chÃnh xÃĄc váŧ dáŧą bÃĄo là thášĨp. ChÚng ta cᚧn xem xÃĐt RI ÄÆ°áŧĢc giášĢi thÃch báŧi 2
biášŋn là Alpha và LY, vášy trong 2 biášŋn nà y biášŋn nà o cÃģ hiáŧu quášĢ dáŧą bÃĄo cho RI
cao hÆĄn? Và cáŧĨ tháŧ là máŧĐc Äáŧ dáŧą bÃĄo ÄÆ°áŧĢc ÄÃĄnh giÃĄ nhÆ° thášŋ nà o? ChÚng ta cᚧn xem
xÃĐt háŧ sáŧ q2, ÄÆ°áŧĢc tÃnh bášąng cÃīng tháŧĐc sau:
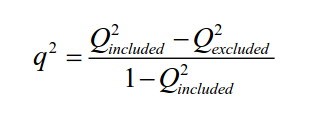
Trong
ÄÃģ:
âĒ Q2included là háŧ sáŧ Q2
cáŧ§a mÃī hÃŽnh gáŧc
âĒ Q2excluded là háŧ sáŧ Q2
cáŧ§a mÃī hÃŽnh ÄÃĢ loᚥi biášŋn tiáŧm ášĐn Äang cᚧn ÄÃĄnh giÃĄ q2
|
|
RI |
|
Alpha |
q2 = ? |
|
LY |
q2 = ? |
MÃī
hÃŽnh loᚥi biášŋn Alpha:
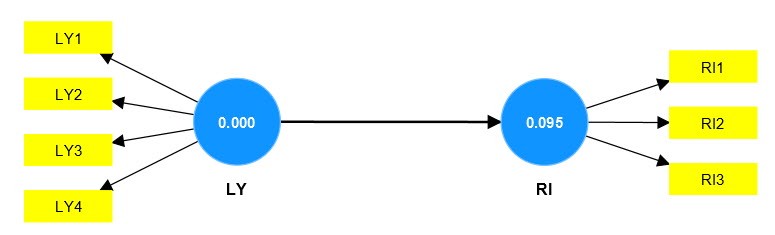
MÃī
hÃŽnh loᚥi biášŋn LY:

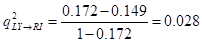
|
|
RI |
|
Alpha |
0.093 â hiáŧu quášĢ dáŧą bÃĄo
áŧ máŧĐc thášĨp |
|
LY |
0.028 â hiáŧu quášĢ dáŧą bÃĄo
áŧ máŧĐc thášĨp |
DÆ°áŧi ÄÃĒy là cÃĄc khung tiÊu chuášĐn
ÄÃĄnh giÃĄ q2 ÄÆ°áŧĢc trÃch dášŦn táŧŦ VÅĐ HáŧŊu Thà nh và Nguyáŧ
n Minh HÃ (2023).
|
ÄÃĄnh giÃĄ hiáŧu quášĢ dáŧą bÃĄo
cáŧ§a máŧt biášŋn giášĢi thÃch |
|
|
q2 < 0.02 |
KhÃīng cÃģ hiáŧu quášĢ dáŧą bÃĄo |
|
0.02 âĪ q2 <
0.15 |
Hiáŧu quášĢ dáŧą bÃĄo thášĨp |
|
0.15 âĪ q2 < 0.35 |
Hiáŧu quášĢ dáŧą bÃĄo trung
bÃŽnh |
|
q2 âĨ 0.35 |
Hiáŧu quášĢ dáŧą bÃĄo cao |
TÃ i
liáŧu tham khášĢo
Hair, J., & Alamer, A. (2022).
Partial Least Squares Structural Equation Modeling (PLS-SEM) in second language
and education research: Guidelines using an applied example. Research
Methods in Applied Linguistics, 1(3), 100027.
VÅĐ HáŧŊu Thà nh, & Nguyáŧ n Minh Hà . (2023). GiÃĄo trÃŽnh phÃĒn tÃch dáŧŊ liáŧu ÃĄp dáŧĨng mÃī hÃŽnh PLS - SEM (1st ed.). NXB ÄH Quáŧc Gia Tp HCM.




