R2 và R2 hiáŧu cháŧnh, Ã―
nghÄĐa và sáŧą khÃĄc biáŧt
1. Äáŧnh nghÄĐa
1.1. R2 (Háŧ sáŧ xÃĄc Äáŧnh)
Äáŧnh nghÄĐa: R2 tháŧ hiáŧn táŧ· láŧ phᚧn
trÄm cáŧ§a táŧng phÆ°ÆĄng sai cáŧ§a biášŋn pháŧĨ thuáŧc (biášŋn Äᚧu ra) ÄÆ°áŧĢc giášĢi thÃch báŧi
cÃĄc biášŋn Äáŧc lášp (biášŋn Äᚧu và o) trong mÃī hÃŽnh. GiÃĄ tráŧ cáŧ§a R2 dao Äáŧng táŧŦ 0 Äášŋn
1 (hoáš·c táŧŦ 0% Äášŋn 100%).
CÃīng tháŧĐc tÃnh R2 nhÆ° sau:

Trong ÄÃģ, SSresidual
là táŧng bÃŽnh phÆ°ÆĄng phᚧn dÆ° và SStotal là táŧng bÃŽnh phÆ°ÆĄng táŧng
tháŧ.
à nghÄĐa: R2 cà ng cao, mÃī hÃŽnh
cà ng cÃģ khášĢ nÄng giášĢi thÃch sáŧą biášŋn Äáŧng cáŧ§a biášŋn pháŧĨ thuáŧc. Tuy nhiÊn, cháŧ sáŧ
nà y khÃīng tÃnh Äášŋn sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp trong mÃī hÃŽnh. Do ÄÃģ, cÃģ tháŧ dášŦn Äášŋn
viáŧc ÄÃĄnh giÃĄ quÃĄ cao máŧĐc Äáŧ phÃđ háŧĢp cáŧ§a mÃī hÃŽnh khi thÊm nhiáŧu biášŋn và o.
1.2. R2 hiáŧu cháŧnh
(Adjusted R2)
Äáŧnh nghÄĐa: R2 hiáŧu cháŧnh lÃ
phiÊn bášĢn Äiáŧu cháŧnh cáŧ§a R2, ÄÆ°áŧĢc tÃnh toÃĄn thÊm yášŋu táŧ sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp
và kÃch thÆ°áŧc mášŦu Äáŧ trÃĄnh viáŧc mÃī hÃŽnh tráŧ nÊn quÃĄ pháŧĐc tᚥp (overfitting) khi
thÊm nhiáŧu biášŋn Äáŧc lášp.
CÃīng tháŧĐc tÃnh R2 hiáŧu cháŧnh nhÆ° sau:
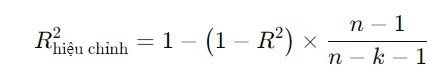
âĒ n là sáŧ lÆ°áŧĢng quan sÃĄt (kÃch thÆ°áŧc mášŦu),
âĒ k là sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp.
à nghÄĐa: R2 hiáŧu cháŧnh thÆ°áŧng
thášĨp hÆĄn R2, Äáš·c biáŧt khi sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp tÄng lÊn. NÃģ cháŧ tÄng khi biášŋn
Äáŧc lášp máŧi tháŧąc sáŧą cÃģ Ã― nghÄĐa trong viáŧc giášĢi thÃch biášŋn pháŧĨ thuáŧc.
2. Sáŧą khÃĄc biáŧt giáŧŊa
R2 và R2 hiáŧu cháŧnh
TÃĄc Äáŧng cáŧ§a biášŋn sáŧ
và kÃch thÆ°áŧc mášŦu: R2 hiáŧu cháŧnh xem xÃĐt sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp và kÃch thÆ°áŧc mášŦu, trong khi
R2 thÃŽ khÃīng. Do ÄÃģ, R2 hiáŧu cháŧnh cung cášĨp ÄÃĄnh giÃĄ chÃnh xÃĄc hÆĄn váŧ máŧĐc Äáŧ
phÃđ háŧĢp cáŧ§a mÃī hÃŽnh, Äáš·c biáŧt khi so sÃĄnh cÃĄc mÃī hÃŽnh váŧi sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp
khÃĄc nhau.
TÄng trÆ°áŧng giÃĄ tráŧ: Khi thÊm biášŋn Äáŧc lášp
và o mÃī hÃŽnh, R2 thÆ°áŧng tÄng bášĨt káŧ biášŋn ÄÃģ cÃģ tháŧąc sáŧą cášĢi thiáŧn mÃī hÃŽnh hay
khÃīng. NgÆ°áŧĢc lᚥi, R2 hiáŧu cháŧnh cháŧ tÄng nášŋu biášŋn máŧi tháŧąc sáŧą háŧŊu Ãch.
TÃģm lᚥi, khi so sÃĄnh
cÃĄc mÃī hÃŽnh, Äáš·c biáŧt là khi sáŧ lÆ°áŧĢng biášŋn Äáŧc lášp khÃĄc nhau, R2 hiáŧu cháŧnh thÆ°áŧng
ÄÆ°áŧĢc Æ°a chuáŧng hÆĄn vÃŽ nÃģ cung cášĨp cÃĄi nhÃŽn tháŧąc tášŋ hÆĄn váŧ khášĢ nÄng dáŧą bÃĄo cáŧ§a
mÃī hÃŽnh.
3. TÃ i liáŧu tham khášĢo
Kutner, M. H.,
Nachtsheim, C. J., Neter, J., & Li, W. (2005). Applied linear
statistical models. McGraw-hill.



