Hó₤ãNG DäˆN PHûN TûCH T-TEST Vû ONE-WAY ANOVA
áã cû° kiä¢n thãˋc tãt vû thiä¢t thãÝc nhäËt vã cûÀc phó¯óÀng phûÀp thãng kûˆ ã mãˋc cóÀ bäÈn, cûÀ nhûÂn chû¤ng tûÇi khuyûˆn cûÀc bäÀn nûˆn áãc qua bã sûÀch cãÏa Hoû ng Trãng vû Chu Nguyã
n Mãng Ngãc áó¯Ã£Èc xuäËt bäÈn nám 2008. Chû¤ng tûÇi áûÀnh giûÀ räÝng, bã sûÀch nû y (gãm 2 täÙp cóÀ bäÈn vû nûÂng cao) lû kiä¢n thãˋc cûÇ áãng vû sû¤c tûÙch nhäËt cho tãi nay. CûÀc anh chã häÀn chä¢ tham khäÈo kiä¢n thãˋc trûˆn mäÀng, mû˜nh lû m nghiûˆn cãˋu cûÀi gû˜ céˋng cäÏn phäÈi cû° nguãn dä¨n khoa hãc thû˜ mãi thuyä¢t phãËc.
I. Lû THUYäƒT Có BäÂN
T-Test vû One-Way ANOVA lû hai phó¯óÀng phûÀp thãng kûˆ
phã biä¢n áó¯Ã£Èc sã٠dãËng áã kiãm tra sÃ£Ý khûÀc biãt giã₤a cûÀc nhû°m dã₤ liãu. Dó¯Ã£i áûÂy
lû phûÂn tûÙch nhanh vã cÃ¤È hai phó¯óÀng phûÀp nû y:
1. T-Test (Kiãm áãnh T):
T-Test lû mãt phó¯óÀng phûÀp thãng kûˆ dû¿ng áã kiãm tra
xem cû° sÃ£Ý khûÀc biãt cû° û§ ngháˋa giã₤a hai nhû°m dã₤ liãu hay khûÇng. T-Test áûÀnh giûÀ
sÃ£Ý khûÀc biãt giã₤a cûÀc trung bû˜nh cãÏa hai nhû°m vû xûÀc áãnh xem liãu sÃ£Ý khûÀc biãt
nû y cû° thã áó¯Ã£Èc coi lû cû° û§ ngháˋa thãng kûˆ hay khûÇng.
Cû° hai loäÀi chûÙnh cãÏa T-Test:
ã T-Test áãc läÙp (Independent T-Test): Sã٠dãËng khi chû¤ng
ta muãn so sûÀnh trung bû˜nh cãÏa mãt biä¢n sã giã₤a hai nhû°m áãc läÙp (khûÇng phÃ£Ë thuãc
lä¨n nhau).
ã T-Test phÃ£Ë thuãc (Paired T-Test): Sã٠dãËng khi chû¤ng
ta muãn so sûÀnh trung bû˜nh cãÏa mãt biä¢n sã trong cû¿ng mãt nhû°m trong hai thãi
áiãm khûÀc nhau.
ã MãËc áûÙch cãÏa T-Test lû kiãm tra xem sÃ£Ý khûÀc biãt giã₤a cûÀc trung bû˜nh cû° áÃ£Ï lãn áã coi lû cû° û§ ngháˋa thãng kûˆ hay khûÇng.
Khi chäÀy kiãm áãnh T-test, cûÀc bäÀn áãi chiä¢u vãi bäÈng sau áûÂy áã kä¢t luäÙn (Hoû ng trãng vû ChûÂu Nguyã n Mãng Ngãc, 2008):
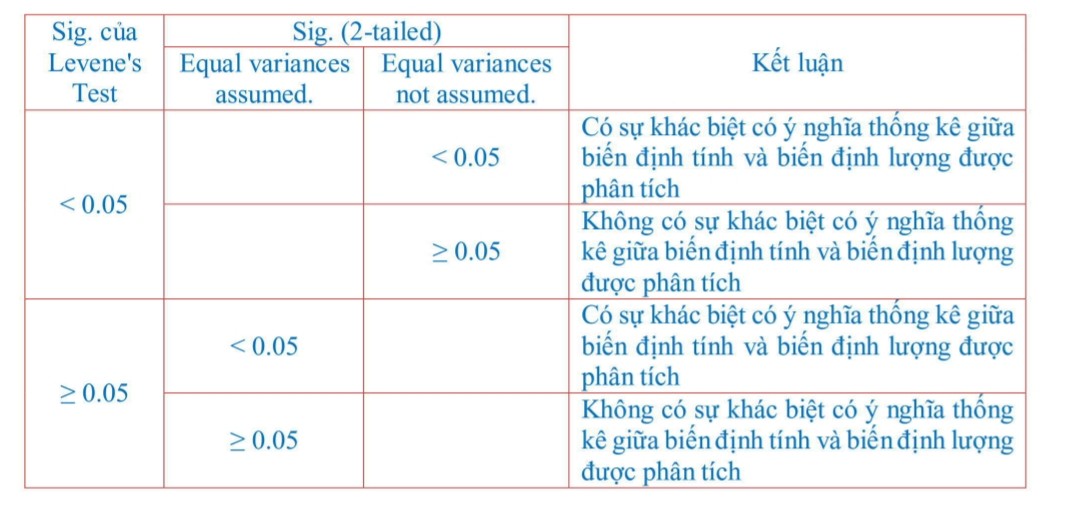
Ló¯u û§ räÝng, T-test chã thãÝc hiãn so sûÀnh theo cäñp. Nûˆn áãi vãi cûÀc biä¢n cäÏn kiãm áãnh sÃ£Ý khûÀc biãt mû cû° nhiãu hóÀn 2 nhû°m thû˜ chû¤ng ta phäÈi thãÝc hiãn tã¨ng cäñp mãt. Viãc nû y sä§ tãn thãi gian, vû mãˋc áã chûÙnh xûÀc cãÏa kä¢t quÃ¤È sä§ khûÇng cûýn áäÈm bäÈo áã tin cäÙy 95%. Do áû°, trong tró¯Ã£ng hãÈp nû y, chû¤ng ta sä§ chuyãn qua kiãm áãnh One-way ANOVA. Kiãm áãnh nû y sä§ giû¤p chû¤ng ta thãÝc hiãn so sûÀnh cûÀc nhû°m cû¿ng mãt lû¤c.
2. One-Way ANOVA (PhûÂn tûÙch phó¯óÀng sai mãt chiãu):
One-Way ANOVA lû mãt phó¯óÀng phûÀp thãng kûˆ áó¯Ã£Èc sã٠dãËng
áã kiãm tra sÃ£Ý khûÀc biãt giã₤a ba hoäñc nhiãu hóÀn cûÀc nhû°m dã₤ liãu. Nû° áûÀnh giûÀ
xem cû° sÃ£Ý khûÀc biãt û§ ngháˋa giã₤a trung bû˜nh cãÏa cûÀc nhû°m dã₤ liãu hay khûÇng.
One-Way ANOVA giÃ¤È áãnh räÝng cûÀc nhû°m dã₤ liãu áó¯Ã£Èc
kiãm tra áãu cû° phûÂn phãi chuäˋn vû cû° phó¯óÀng sai bäÝng nhau. Nä¢u kä¢t quÃ¤È phûÂn
tûÙch cho thäËy cû° sÃ£Ý khûÀc biãt û§ ngháˋa giã₤a ûÙt nhäËt hai trong sã cûÀc nhû°m, chû¤ng
ta cû° thã thãÝc hiãn cûÀc phûÂn tûÙch thûˆm áã xûÀc áãnh nhû°m nû o chãˋa sÃ£Ý khûÀc biãt.
ã MãËc áûÙch cãÏa One-Way ANOVA lû kiãm tra sÃ£Ý khûÀc biãt
giã₤a cûÀc trung bû˜nh cãÏa ba hoäñc nhiãu nhû°m áã xûÀc áãnh xem liãu cû° ûÙt nhäËt mãt
nhû°m cû° sÃ£Ý khûÀc biãt û§ ngháˋa so vãi cûÀc nhû°m khûÀc hay khûÇng.
Trong cÃ¤È T-Test vû One-Way ANOVA, mãËc áûÙch cuãi cû¿ng lû áûÀnh giûÀ sÃ£Ý khûÀc biãt giã₤a cûÀc nhû°m dã₤ liãu vû xûÀc áãnh liãu sÃ£Ý khûÀc biãt nû y cû° û§ ngháˋa thãng kûˆ hay khûÇng. Ló¯u û§ räÝng, tró¯Ã£c khi thãÝc hiãn bäËt kã° phûÂn tûÙch nû o, chû¤ng cäÏn kiãm tra cûÀc giÃ¤È áãnh cãÏa phûÂn phãi dã₤ liãu vû phó¯óÀng sai, áã áäÈm bäÈo tûÙnh hãÈp lû§ vû áûÀng tin cäÙy cãÏa kä¢t quÃ¤È phûÂn tûÙch. Viãc áûÀnh giûÀ phûÂn phãi chuäˋn cãÏa dã₤ liãu anh chã xem thûˆm täÀi bû i viä¢t céˋ hóÀn cãÏa chû¤ng tûÇi ã áûÂy. Trong nãi dung bû i viä¢t nû y, chû¤ng ta mäñc áãnh dã₤ liãu áäÈm bäÈo tûÙnh phûÂn phãi chuäˋn.
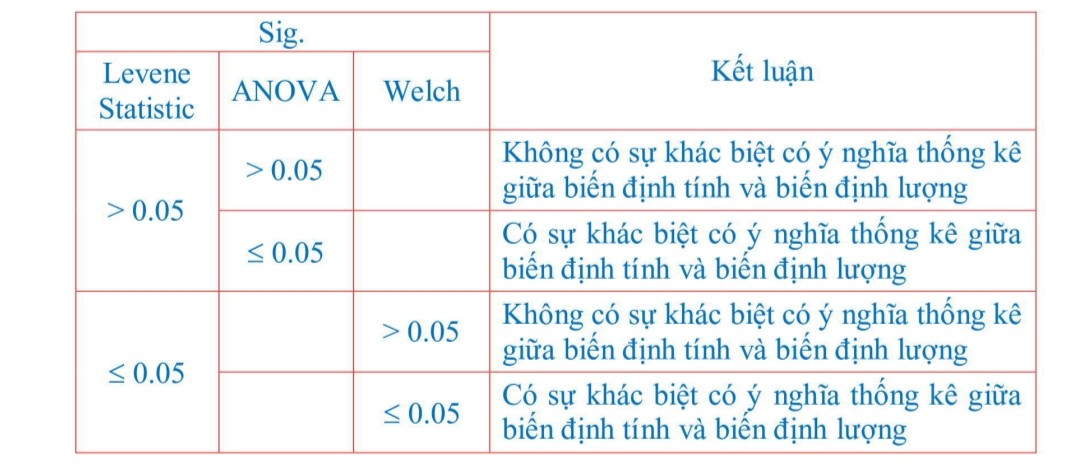
II. THã¯C HûNH PHûN TûCH
Tiä¢p theo sau áûÂy, chû¤ng ta sä§ tiä¢n hû nh phûÂn tûÙch
mä¨u T-test vû One-way ANOVA. Biä¢n phÃ£Ë thuãc cãÏa chû¤ng ta lû RI (û áãnh mua läñp
läÀi säÈn phäˋm), vû cûÀc biä¢n nhûÂn khäˋu hãc bao gãm: Nhû°m mua, Giãi tûÙnh, Tuãi vû
Trû˜nh áã hãc väËn. áäñc áiãm cãÏa cûÀc biä¢n NhûÂn khäˋu hãc nhó¯ BäÈng bûˆn dó¯Ã£i.
Ló¯u û§ räÝng, trong phäÀm vi bû i viä¢t nû y, chû¤ng tûÇi sä§
khûÇng ái sûÂu vû o cûÀch chäÀy phûÂn tûÙch bäÝng phäÏn mãm SPSS, anh chã quan tûÂm cû° thã
tû˜m áãc tû i liãu áó¯Ã£Èc Dãch vÃ£Ë sã liãu Lûˆ Minh chia sä£ täÀi áûÂy.
|
Tûˆn biä¢n |
MûÈ hû°a |
áäñc áiãm |
|
Nhû°m mua |
1 |
Nhû°m mua ã chÃ£È truyãn thãng |
|
2 |
Nhû°m mua ã cûÀc cãÏa hû ng tiãn lãÈi hoäñc siûˆu thã |
|
|
Giãi tûÙnh |
1 |
Nam |
|
2 |
Nã₤ |
|
|
Tuãi |
1 |
ãÊ 22 tuãi |
|
2 |
23 áä¢n 30 tuãi |
|
|
3 |
31 áä¢n 45 tuãi |
|
|
4 |
Trûˆn 45 tuãi |
|
|
Trû˜nh áã hãc väËn |
1 |
ãÊ THPT |
|
2 |
Trung cäËp/Cao áä°ng |
|
|
3 |
áäÀi hãc |
|
|
4 |
Sau áäÀi hãc |
Chû¤ng ta ló¯u û§ räÝng, kiãm
áãnh T-test chã thãÝc hiãn áãi vãi cûÀc biä¢n cû° t㨠2 nhû°m trã xuãng, vãi cûÀc biä¢n
t㨠3 nhû°m trã lûˆn thû˜ cäÏn chäÀy kiãm áãnh One way Anova. Trong tró¯Ã£ng hãÈp vûÙ dãË
nû y, chû¤ng ta chäÀy T-test cho cûÀc biä¢n lû Nhû°m mua vû Giãi tûÙnh, cûÀc biä¢n cûýn läÀi
lû Tuãi vû Trû˜nh áã hãc väËn sä§ áó¯Ã£Èc chäÀy kiãm áãnh One way Anova. ã áûÂy, chû¤ng
tûÇi chã trû˜nh bû y mä¨u chäÀy cho cûÀc biä¢n lû Nhû°m mua vû Trû˜nh áã hãc väËn.
1. Nhû°m mua
áã chäÀy kiãm áãnh T-test cho Nhû°m mua, chû¤ng ta thãÝc hiãn cûÀc bó¯Ã£c nhó¯ hû˜nh bûˆn dó¯Ã£i.
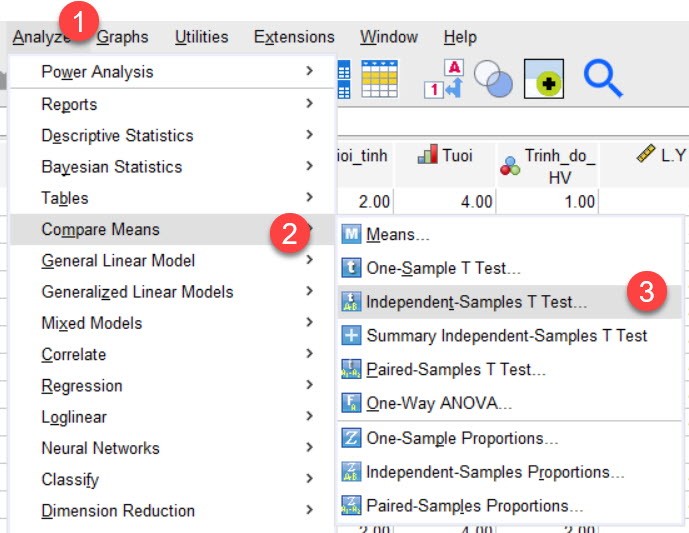
Sau áû° áãc kä¢t quäÈ.
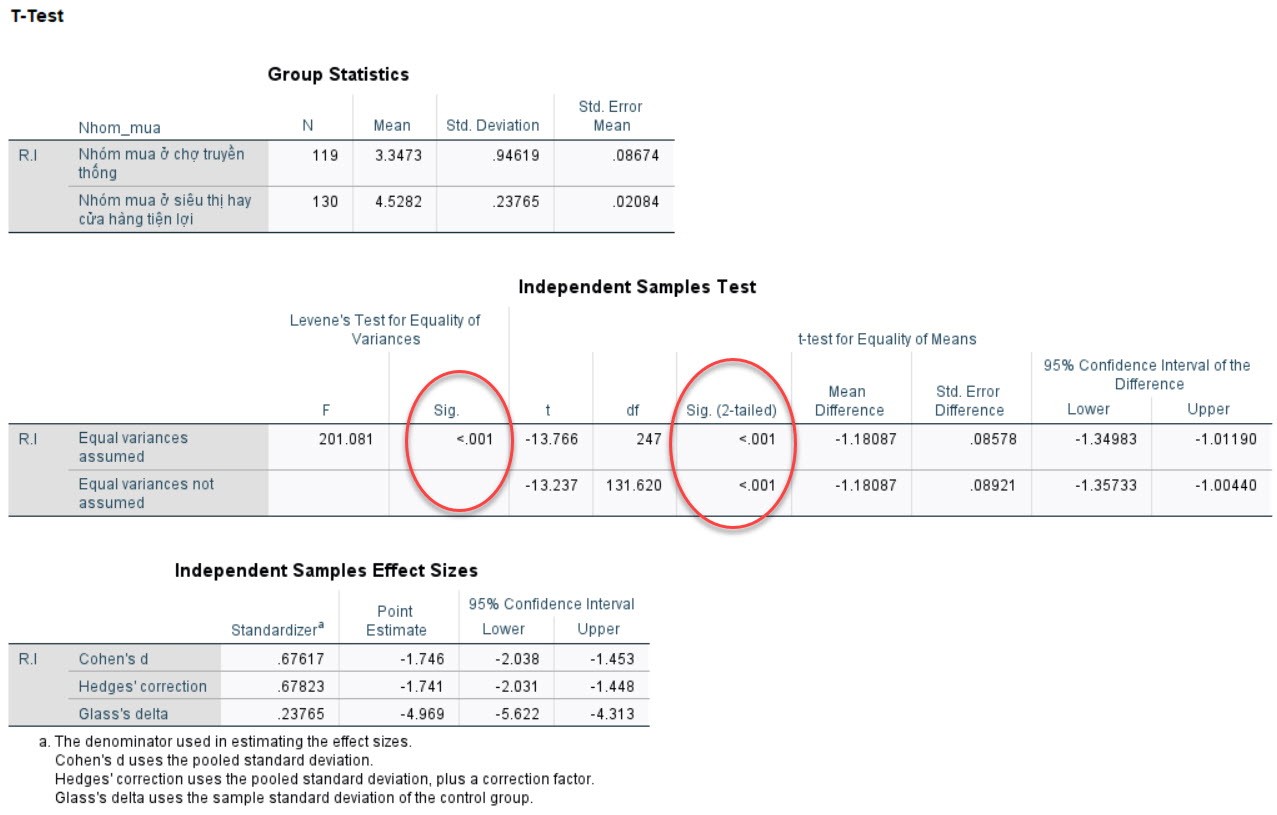
CûÀc giûÀ trã Sig. áãu áäÀt mãˋc û§ ngháˋa thãng kûˆ (ãÊ 5%)
nûˆn kä¢t luäÙn räÝng, Nhû°m mua cû° sÃ£Ý khûÀc biãt cû° û§ ngháˋa thãng kûˆ áãi vãi û áãnh
mua läñp läÀi cãÏa khûÀch hû ng. áã áûÀnh giûÀ thûˆm vã û§ áãnh mua läñp läÀi cãÏa 2 nhû°m
mua (nhû°m nû o cû° û§ áãnh mua läñp läÀi cao hóÀn) mû khûÇng cäÏn chäÀy MGA, chû¤ng ta thãÝc
hiãn nhó¯ sau. Chû¤ng ta copy bäÈng Group Statistics vû o Excel, sau áû° vä§ áã thã vã
giûÀ trã MEAN nhó¯ hû˜nh dó¯Ã£i. TûÙ nã₤a phûÙa sau mû˜nh sä§ trû˜nh bû y chi tiä¢t cûÀch tûÙnh
giûÀ trã Mean nû y lû nhó¯ thä¢ nû o. Chû¤ng ta täÀm hiãu giûÀ trã mean nû y lû giûÀ trã
mean cãÏa biä¢n phÃ£Ë thuãc RI tó¯óÀng ãˋng vãi tã¨ng nhû°m mua.
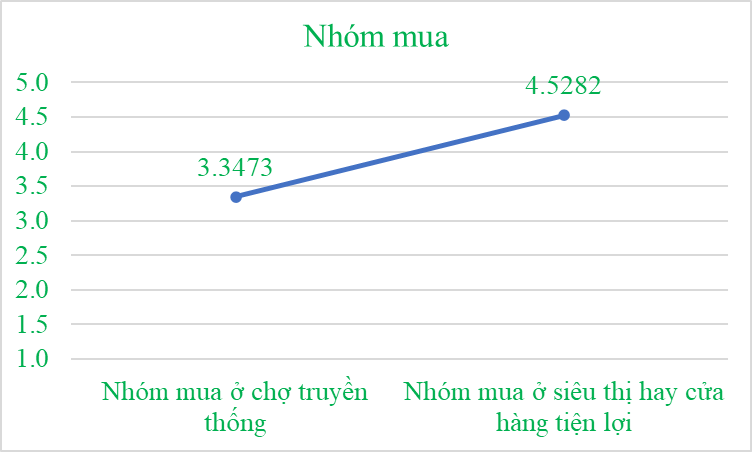
T㨠áã thã cû° thã thäËy áó¯Ã£Èc räÝng, Nhû°m mua ã siûˆu thã
hay cãÙa hû ng tiãn lãÈi cû° khuynh hó¯Ã£ng mua läñp läÀi säÈn phäˋm cao hóÀn Nhû°m mua ã
chÃ£È truyãn thãng.
2. Trû˜nh áã hãc väËn
áãi vãi Trû˜nh áã hãc väËn, chû¤ng ta sä§ thãÝc hiãn kiãm áãnh One way Anova. CûÀc bó¯Ã£c thãÝc hiãn áó¯Ã£Èc triãn khai nhó¯ hû˜nh dó¯Ã£i.
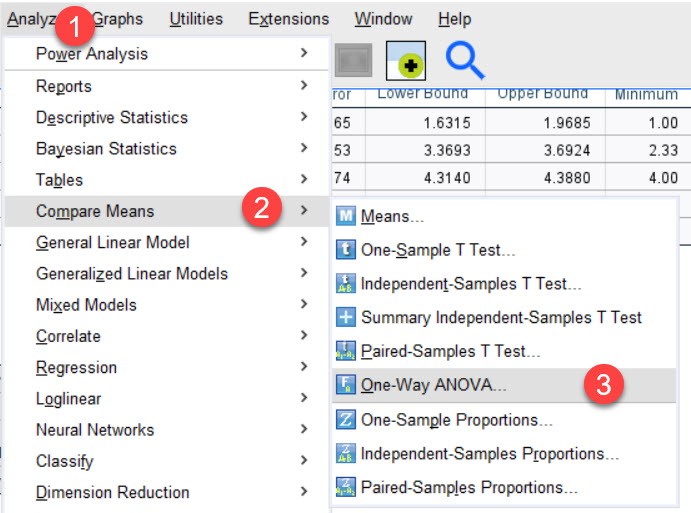
ã phäÏn option chû¤ng ta lãÝa chãn nhó¯ hû˜nh, cûÀc mãËc
khûÀc cãˋ áã mäñc áãnh nhûˋ.
áãc kä¢t quäÈ
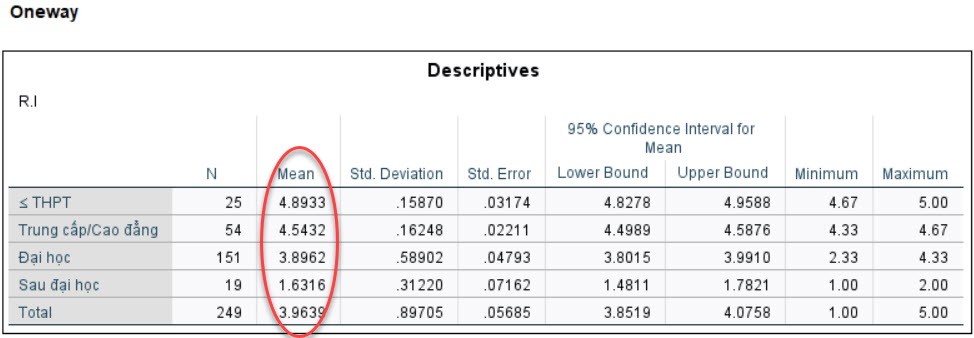
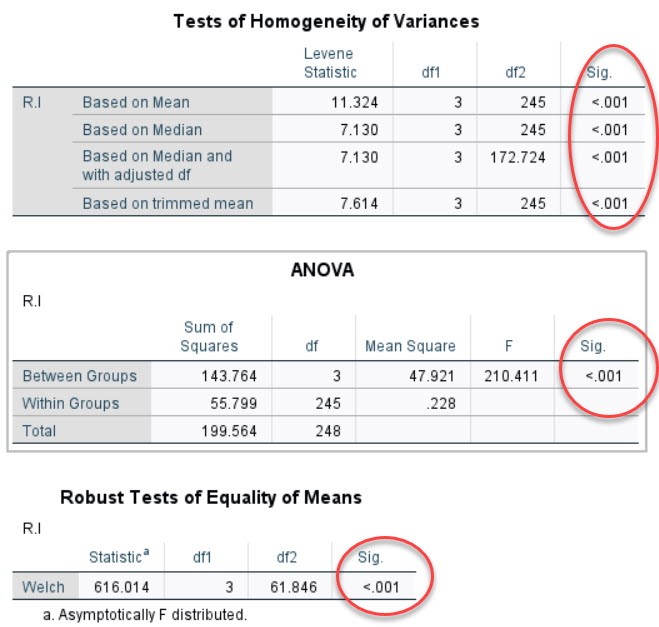
CûÀc giûÀ trã Sig. áãu áäÀt mãˋc û§ ngháˋa thãng kûˆ (ãÊ 5%), nûˆn kä¢t luäÙn áó¯Ã£Èc räÝng, Trû˜nh áã hãc väËn cû° sÃ£Ý khûÀc biãt cû° û§ ngháˋa thãng kûˆ vãi û áãnh mua läñp läÀi säÈn phäˋm cãÏa khûÀch hû ng. CÃ£Ë thã chû¤ng ta tiä¢n hû nh thûˆm phûÂn tûÙch áã thã vã giûÀ trã mean nhó¯ sau. Anh chã céˋng copy bäÈng thãng kûˆ nhû°m vû o Excel vû vä§ áã thã cho giûÀ trã mean nhûˋ.
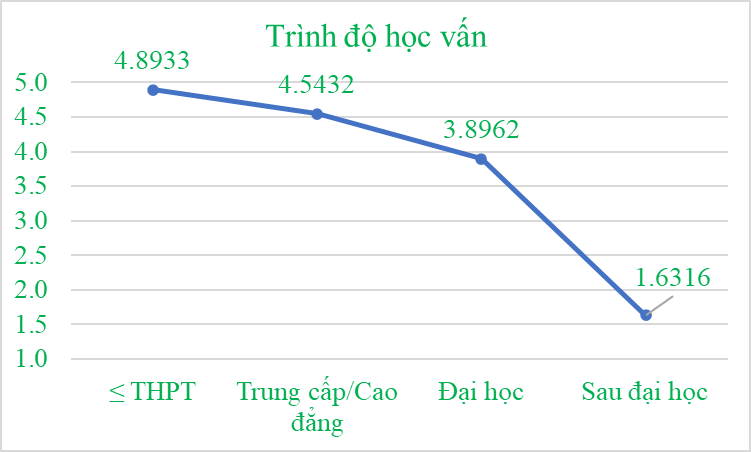
Nhû˜n vû o áã thã chû¤ng ta cû° thã thäËy áó¯Ã£Èc räÝng, trû˜nh áã cû ng thäËp ngó¯Ã£i ta cû° khuynh hó¯Ã£ng mua läñp läÀi cû ng nhiãu.
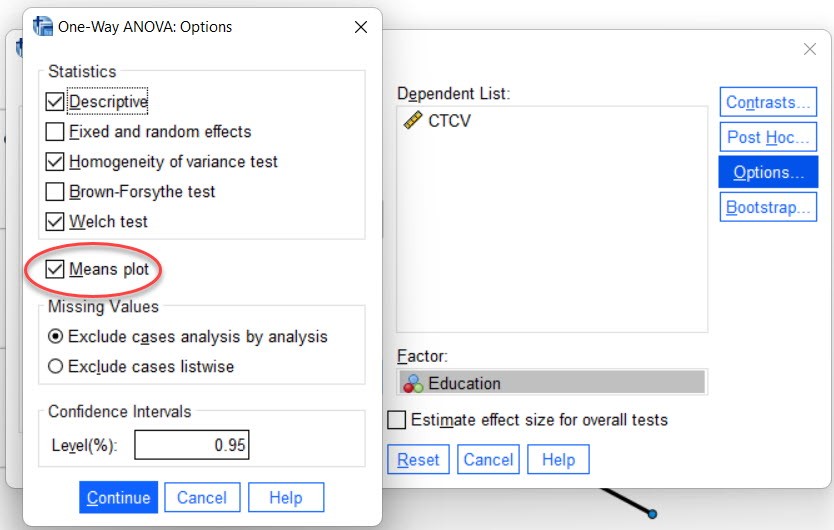
Nä¢u khûÇng muãn thã hiãn áã thã bäÝng Excel cho dã nhû˜n thû˜ chû¤ng ta cû° thã sã٠dãËng cûÇng cÃ£Ë SPSS áã vä§ áã thã giûÀ trã mean céˋng áó¯Ã£Èc nhûˋ. áã vä§ áã thã khi lãÝa chãn phûÂn tûÙch T-test hay Anova, anh chã nhã click chuãt chãn Means plot nhó¯ hû˜nh bûˆn dó¯Ã£i lû áó¯Ã£Èc.
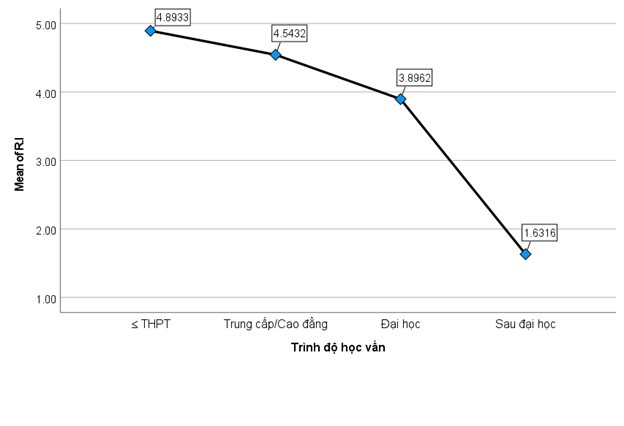
III. NhäÙn xûˋt chung vû cûÀch tûÙnh giûÀ trã mean trong
bäÈng Group Statistics
áãi vãi phûÂn tûÙch T-test vû One-way Anova chû¤ng ta
céˋng chã áûÀnh giûÀ áó¯Ã£Èc sóÀ bã vû khuynh hó¯Ã£ng cãÏa cûÀc nhû°m biä¢n áãi vãi biä¢n chû¤ng
ta so sûÀnh. Cûýn áã phûÂn tûÙch sûÂu hóÀn, tã¨ng nhû°m biä¢n cû° äÈnh hó¯Ã£ng nhó¯ thä¢ nû o
trong mûÇ hû˜nh nghiûˆn cãˋu thû˜ chû¤ng ta cäÏn phäÈi tiä¢n hû nh cûÀc phûÂn tûÙch chuyûˆn sûÂu
nhó¯ MGA.
Giã chû¤ng ta sä§ tû˜m hiãu cûÀch chó¯óÀng trû˜nh tûÙnh giûÀ
trã mean trong bäÈng thãng kûˆ lû nhó¯ thä¢ nû o.
GiûÀ trã mean trong bäÈng thãng kûˆ nhû°m biä¢n lû giûÀ trã mean cãÏa biä¢n áãi tó¯Ã£Èng so sûÀnh (ã áûÂy lû biä¢n RI ã û áãnh mua läñp läÀi) theo tã¨ng nhû°m biä¢n. VûÙ dãË, mû˜nh sä§ tûÙnh giûÀ trã mean cho phûÂn tûÙch One way Anova cãÏa biä¢n Trû˜nh áã hãc väËn. Tró¯Ã£c tiûˆn, chû¤ng ta copy cãt biä¢n Trû˜nh áã hãc väËn vû biä¢n RI vû o file excel.
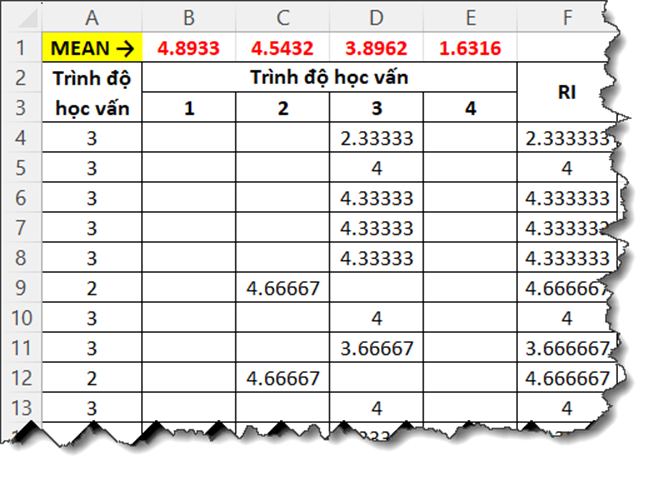
CûÇng thãˋc mû˜nh sã٠dãËng trong excel nhó¯ sau: Chû¤ng
ta chã cû i cûÇng thãˋc nhó¯ ã ûÇ B4 rãi sau áû° kûˋo thÃ¤È lû xong.

Nhó¯ väÙy tãi áûÂy chû¤ng tûÇi täÀm xong phäÏn hó¯Ã£ng dä¨n cûÀc anh chã phûÂn tûÙch cûÀc kiãm áãnh T-test vû One way Anova. Anh chã nû o cû° nhu cäÏu vã sã liãu thû˜ hûÈy liûˆn hã vãi Dãch vÃ£Ë sã liãu Lûˆ Minh nhûˋ. TrûÂn trãng cäÈm óÀn.
Mãt sã giäÈi thûÙch cóÀ bäÈn cho T-test vû Anova One-way chû¤ng tûÇi xin phûˋp áó¯Ã£Èc trûÙch nguyûˆn ván cãÏa George, D., & Mallery, P. (2021).
_1-20230807145641.jpg)
Tû i liãu tham khäÈo
George, D., &
Mallery, P. (2022). IBM SPSS statistics 27 step by step: A simple guide and
reference. Routledge. https://doi.org/10.4324/9781003205333
Hoû ng Trãng vû Chu Nguyã n Mãng Ngãc. (2008). PhûÂn tûÙch dã₤ liãu nghiûˆn cãˋu vãi SPSS. NXB Hãng áãˋc.
Salcedo, J., &
McCormick, K. (2023). SPSS statistics for dummies. John Wiley &
Sons.




