ASSESSING NORMALITY OF DATA USING SPSS AMOS
(─É├üNH GI├ü PH├éN PHß╗ÉI CHUß║©N Cß╗”A Dß╗« LIß╗åU)
Trong b├Āi n├Āy, ch├║ng ta sß║Į t├¼m hiß╗āu kß╗╣ thuß║Łt kiß╗ām tra t├Łnh ph├┤i phß╗æi cß╗¦a dß╗» liß╗ću. Ph├ón phß╗æi chuß║®n l├Ā mß╗Öt ph├ón phß╗æi x├Īc suß║źt li├¬n tß╗źc ─æß╗æi xß╗®ng xung quanh gi├Ī trß╗ŗ trung b├¼nh cß╗¦a n├│, hß║¦u hß║┐t c├Īc quan s├Īt tß║Łp hß╗Żp xung quanh ─æß╗ēnh trung t├óm v├Ā x├Īc suß║źt ─æß╗æi vß╗øi c├Īc gi├Ī trß╗ŗ xa trung b├¼nh giß║Żm dß║¦n theo cß║Ż hai hŲ░ß╗øng. Ph├ón phß╗æi chuß║®n tß║»c (standard normal distribution) l├Ā ph├ón phß╗æi chuß║®n vß╗øi gi├Ī trß╗ŗ trung b├¼nh (╬╝) bß║▒ng 0 v├Ā ─æß╗Ö lß╗ćch chuß║®n (Žā) bß║▒ng 1. Ph├ón phß╗æi chuß║®n c├▓n ─æŲ░ß╗Żc gß╗Źi l├Ā ─æŲ░ß╗Øng cong chu├┤ng (bell curve) v├¼ ─æß╗ō thß╗ŗ cß╗¦a mß║Łt ─æß╗Ö x├Īc suß║źt c├│ dß║Īng chu├┤ng.
Kiß╗ām ─æß╗ŗnh ph├ón phß╗æi chuß║®n l├Ā mß╗Öt bŲ░ß╗øc quan trß╗Źng trong thß╗¦ tß╗źc thß╗æng k├¬ suy luß║Łn, gi├║p ch├║ng ta x├Īc ─æß╗ŗnh ─æŲ░ß╗Żc cŲĪ bß║Żn h├¼nh dß║Īng chung cß╗¦a mß╗Öt ph├ón phß╗æi, tß╗½ ─æ├│ ─æ├Īnh gi├Ī kiß╗ām ─æß╗ŗnh c├│ bß╗ŗ lß╗ćch hay kh├┤ng, v├Ā c├│ ─æß╗Ö lß╗ćch dŲ░ŲĪng hay ├óm. Kiß╗ām ─æß╗ŗnh ph├ón phß╗æi chuß║®n ─æŲ░ß╗Żc sß╗Ł dß╗źng ─æß╗ā kiß╗ām tra xem mß╗Öt tß║Łp hß╗Żp dß╗» liß╗ću c├│ tu├ón theo ph├ón phß╗æi chuß║®n hay kh├┤ng. Nß║┐u tß║Łp hß╗Żp dß╗» liß╗ću tu├ón theo ph├ón phß╗æi chuß║®n, ch├║ng ta c├│ thß╗ā sß╗Ł dß╗źng c├Īc thß╗æng k├¬ li├¬n quan ─æß║┐n ph├ón phß╗æi chuß║®n nhŲ░ kiß╗ām ─æß╗ŗnh t v├Ā ANOVA. Ngo├Āi ra, c├▓n thß╗▒c hiß╗ćn c├Īc thß╗æng k├¬ kh├Īc nhŲ░: gi├Ī trß╗ŗ trung b├¼nh (mean); ─æß╗Ö lß╗ćch chuß║®n (standard deviation); ph├ón vß╗ŗ (percentile); hß╗ć sß╗æ tŲ░ŲĪng quan Pearson (Pearson correlation coefficient); kiß╗ām ─æß╗ŗnh giß║Ż thuyß║┐t vß╗ü gi├Ī trß╗ŗ trung b├¼nh cß╗¦a mß╗Öt mß║½u (t-test). Nß║┐u dß╗» liß╗ću kh├┤ng tu├ón theo ph├ón phß╗æi chuß║®n, ch├║ng ta c├│ thß╗ā sß╗Ł dß╗źng c├Īc phŲ░ŲĪng ph├Īp kh├Īc nhŲ░ kiß╗ām ─æß╗ŗnh Mann-Whitney U hoß║Ęc Kruskal-Wallis. Tuy nhi├¬n, c├Īc phŲ░ŲĪng ph├Īp n├Āy c├│ nhŲ░ß╗Żc ─æiß╗ām l├Ā kh├┤ng nhß║Īy vß╗øi c├Īc gi├Ī trß╗ŗ ngoß║Īi lai v├Ā kh├┤ng cho ph├®p sß╗Ł dß╗źng c├Īc thß╗æng k├¬ li├¬n quan ─æß║┐n ph├ón phß╗æi chuß║®n.
Th├┤ng
thŲ░ß╗Øng ─æß╗ā nhß║Łn biß║┐t mß╗Öt ph├ón phß╗æi chuß║®n trong SPSS c├│ thß╗ā sß╗Ł dß╗źng c├Īc c├Īch sau:
+ Xem biß╗āu ─æß╗ō vß╗øi ─æŲ░ß╗Øng cong chuß║®n
(Histograms with normal curve) vß╗øi dß║Īng h├¼nh chu├┤ng ─æß╗æi xß╗®ng vß╗øi tß║¦n sß╗æ cao nhß║źt
nß║▒m ngay giß╗»a v├Ā c├Īc tß║¦n sß╗æ thß║źp dß║¦n nß║▒m ß╗¤ 2 b├¬n.
+ Vß║Į biß╗āu ─æß╗ō x├Īc suß║źt chuß║®n (normal Q-Q
plot) ŌĆō ph├ón phß╗æi chuß║®n khi biß╗āu ─æß╗ō c├│ quan hß╗ć tuyß║┐n t├Łnh (─æŲ░ß╗Øng thß║│ng).
+ Kiß╗ām tra gi├Ī trß╗ŗ Skewness v├Ā Kurtosis cß╗¦a biß║┐n ─æß╗Öc lß║Łp. Nß║┐u Skewness v├Ā Kurtosis nß║▒m trong khoß║Żng tß╗½ -1 ─æß║┐n 1 th├¼ ph├ón phß╗æi cß╗¦a biß║┐n ─æß╗Öc lß║Łp ─æŲ░ß╗Żc coi l├Ā ph├ón phß╗æi chuß║®n (Hair v├Ā ctg, 2019, p.48). C├▓n theo Collier (2020) th├¼ phß║Īm vi Skewness nß║▒m trong khoß║Żng tß╗½ -2 ─æß║┐n 2, v├Ā Kurtosis nß║▒m trong khoß║Żng tß╗½ -10 ─æß║┐n 10 th├¼ dß╗» liß╗ću ─æŲ░ß╗Żc ─æ├Īnh gi├Ī l├Ā c├│ ph├ón phß╗æi chuß║®n. Nß║┐u dß╗» liß╗ću cß╗¦a bß║Īn kh├┤ng c├│ ph├ón phß╗æi chuß║®n th├¼ sß╗Ł dß╗źng phŲ░ŲĪng ph├Īp Ų░ß╗øc lŲ░ß╗Żng maximum likelihood l├Ā kh├┤ng ─æŲ░ß╗Żc, m├Ā phß║Żi thay thß║┐ bß║▒ng phŲ░ŲĪng ph├Īp Ų░ß╗øc lŲ░ß╗Żng kh├Īc nhŲ░ GLM - general linear model (Collier, 2020, p.166).
Sau
─æ├óy ch├║ng ta sß╗Ł dß╗źng SPSS ─æß╗ā kiß╗ām ─æß╗ŗnh ph├ón phß╗æi chuß║®n cho bß╗Ö dß╗» liß╗ću.
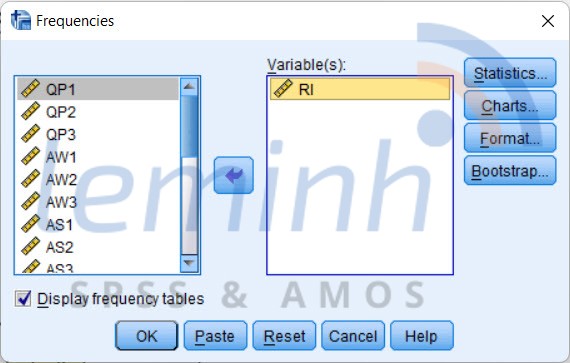
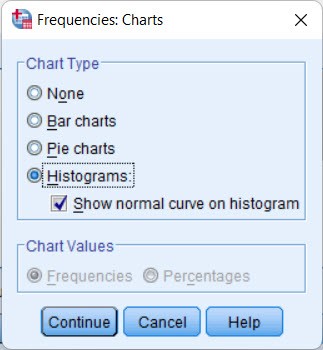
─Éß║¦u ti├¬n, tß║Īi giao diß╗ćn ch├Łnh cß╗¦a SPSS, nhß║źn chß╗Źn Analyze > Descriptive Statistics > FrequenciesŌĆ” ─ÉŲ░a c├Īc biß║┐n cß║¦n kiß╗ām ─æß╗ŗnh v├Āo ├┤ Variable(s). Tiß║┐p tß╗źc nhß║źn chß╗Źn c├Īc lß╗ćnh theo thß╗® tß╗▒ Charts > Histograms > Show normal curve on histogram. Nhß║źn Continue > OK v├Ā chß╗Ø kß║┐t quß║Ż.
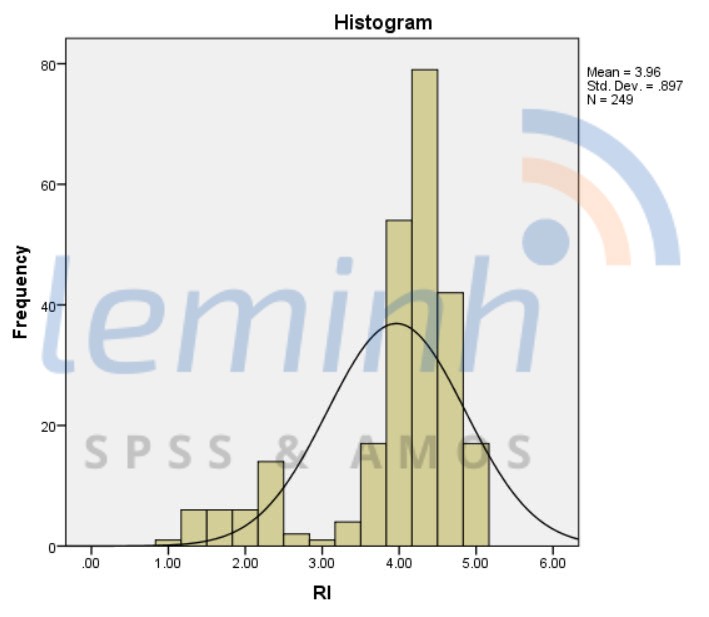
Vß║Į biß╗āu ─æß╗ō ─æŲ░ß╗Øng
cong chuß║®n:
Trên
thanh c├┤ng cß╗ź, nhß║źn chß╗Źn Analyze > Descriptive Statistics > Descriptives.
─ÉŲ░a biß║┐n cß║¦n kiß╗ām ─æß╗ŗnh v├Āo ├┤ Variable(s), nhß║źn chß╗Źn Options. T├Łch chß╗Źn v├Āo 2 ├┤
Kurtosis v├Ā Skewness, chß╗Źn Continue v├Ā nhß║źn OK, sau ─æ├│ chß╗Ø kß║┐t quß║Ż.
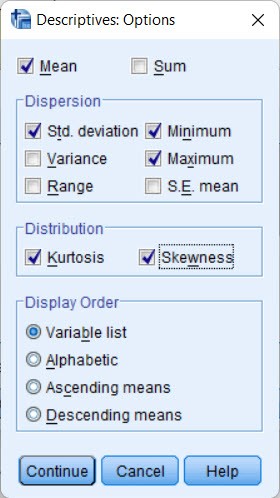

Gi├Ī trß╗ŗ Skewness cß╗¦a biß║┐n ─æß╗Öc lß║Łp l├Ā -1.596 th├¼ c├│ thß╗ā kß║┐t luß║Łn rß║▒ng ph├ón phß╗æi cß╗¦a biß║┐n ─æß╗Öc lß║Łp kh├┤ng phß║Żi l├Ā ph├ón phß╗æi chuß║®n. Tuy nhi├¬n, ─æß╗ā ─æŲ░a ra kß║┐t luß║Łn ch├Łnh x├Īc hŲĪn vß╗ü t├Łnh chuß║®n cß╗¦a ph├ón phß╗æi, bß║Īn c├│ thß╗ā sß╗Ł dß╗źng c├Īc c├Īch kiß╗ām tra kh├Īc nhŲ░ kiß╗ām tra Shapiro-Wilk hoß║Ęc Kolmogorov-Smirnov.
Vß║Į biß╗āu ─æß╗ō x├Īc suß║źt
chuß║®n (Biß╗āu ─æß╗ō Q-Q)
Biß╗āu ─æß╗ō Q-Q cho thß║źy mß╗Öt h├¼nh ß║Żnh
trß╗▒c quan vß╗ü sß╗▒ ph├ón bß╗æ dß╗» liß╗ću, thŲ░ß╗Øng ─æŲ░ß╗Żc sß╗Ł dß╗źng vß╗øi nhß╗»ng nghi├¬n cß╗®u c├│
k├Łch thŲ░ß╗øc mß║½u lß╗øn (>100). C├Īch vß║Į biß╗āu ─æß╗ō Q-Q nhŲ░ sau.
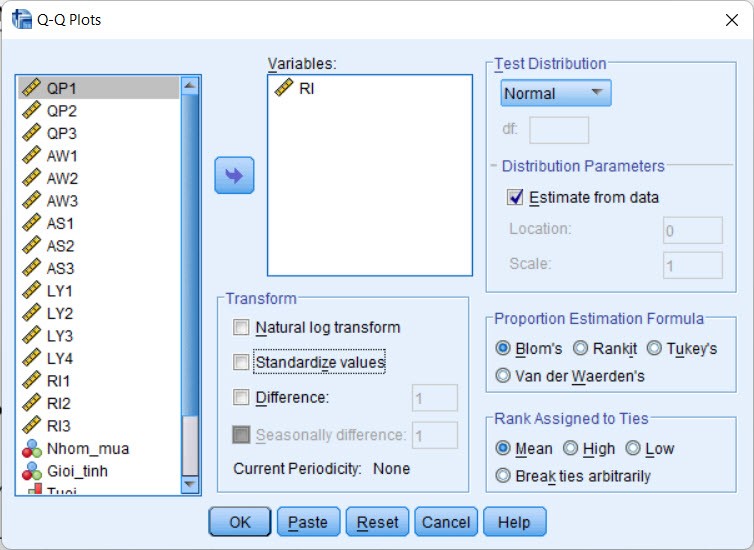
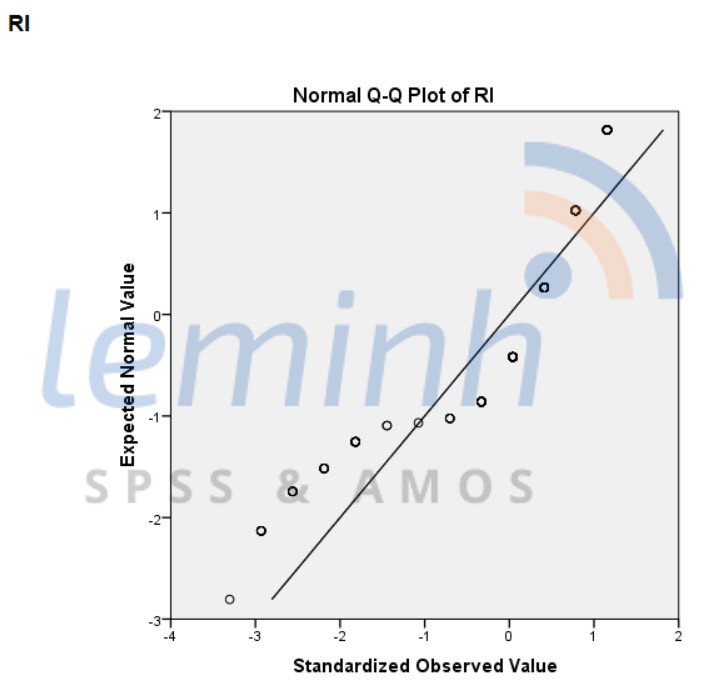
C├│ thß╗ā thß║źy rß║▒ng, c├Īc dß║¦u chß║źm ph├ón bß╗æ c├Īch xa ─æŲ░ß╗Øng xu hŲ░ß╗øng. ─Éiß╗üu n├Āy cung cß║źp th├¬m bß║▒ng chß╗®ng rß║▒ng dß╗» liß╗ću kh├┤ng ─æß║Īt ph├ón phß╗æi chuß║®n. Ch├║ng ta ho├Ān to├Ān c├│ thß╗ā kß║┐t hß╗Żp biß╗āu ─æß╗ō Q-Q n├Āy c├╣ng vß╗øi nhß╗»ng kß║┐t quß║Ż cß╗¦a nhß╗»ng b├Āi kiß╗ām tra thß╗æng k├¬ tr├¬n ─æß╗ā khß║│ng ─æß╗ŗnh chß║»c chß║»n dß╗» liß╗ću n├Āy c├│ l├Ā ph├ón phß╗æi chuß║®n hay kh├┤ng.
Normality Assessment
Trong AMOS ─æß╗ā ─æ├Īnh gi├Ī t├Łnh ph├ón phß╗æi chuß║®n cß╗¦a dß╗» liß╗ću, ch├║ng ta sß╗Ł dß╗źng kß╗╣ thuß║Łt Tests for normality and outliers.
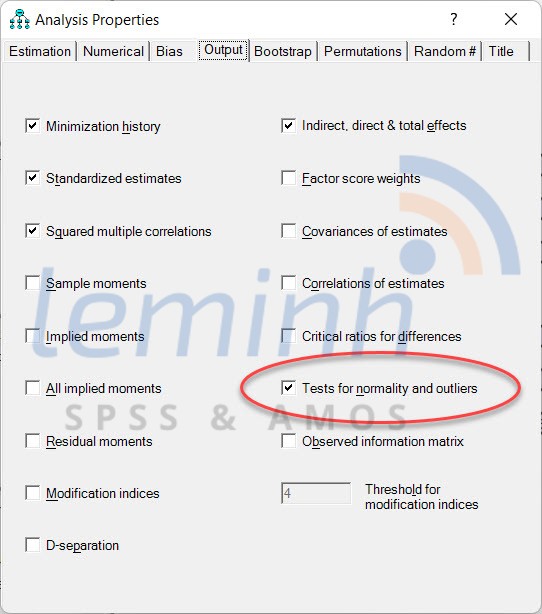
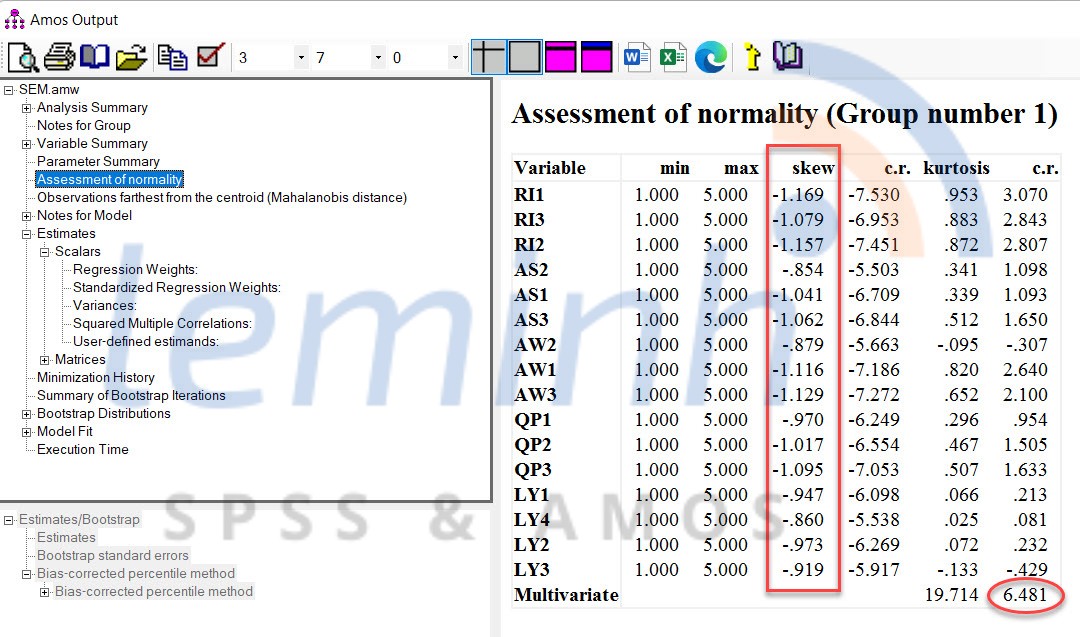
Gi├Ī trß╗ŗ tuyß╗ćt ─æß╗æi cß╗¦a skewness Ōēż 1 th├¼ dß╗» liß╗ću ─æŲ░ß╗Żc ─æ├Īnh gi├Ī l├Ā ph├ón phß╗æi chuß║®n. Tuy nhi├¬n, SEM sß╗Ł dß╗źng C├┤ng cß╗ź MLE (Maximum Likelihood Estimator) nhŲ░ AMOS kh├Ī mß║Īnh vß╗øi skewness c├│ trß╗ŗ tuyß╗ćt ─æß╗æi lß╗øn hŲĪn 1.0 nß║┐u k├Łch thŲ░ß╗øc mß║½u lß╗øn v├Ā V├╣ng tß╗øi hß║Īn (CR) cho ─æß╗Ö lß╗ćch kh├┤ng vŲ░ß╗Żt qu├Ī 8,0. ─Éiß╗üu n├Āy c├│ ngh─®a l├Ā, ch├║ng ta c├│ thß╗ā tiß║┐n h├Ānh ph├ón t├Łch s├óu hŲĪn (SEM) v├¼ c├┤ng cß╗ź Ų░ß╗øc t├Łnh ─æŲ░ß╗Żc sß╗Ł dß╗źng l├Ā MLE. Th├┤ng thŲ░ß╗Øng, k├Łch thŲ░ß╗øc mß║½u lß╗øn hŲĪn 200 ─æŲ░ß╗Żc coi l├Ā ─æß╗¦ lß╗øn trong MLE mß║Ęc d├╣ ph├ón phß╗æi dß╗» liß╗ću kh├┤ng ß╗¤ dß║Īng chuß║®n. ─Éß╗æi vß╗øi kurtosis, phß║Īm vi l├Ā ŌłÆ10 ─æß║┐n +10 th├¼ dß╗» liß╗ću vß║½n ─æŲ░ß╗Żc coi l├Ā ph├ón bß╗æ b├¼nh thŲ░ß╗Øng (Collier, 2020).
C├│ nhiß╗üu c├Īch ─æß╗ā xß╗Ł l├Į dß╗» liß╗ću nhŲ░ x├│a ─æi c├Īc items c├│ ─æß╗Ö lß╗ćch lß╗øn. Tuy nhi├¬n, phŲ░ŲĪng ph├Īp phß╗Ģ biß║┐n nhß║źt gß║¦n ─æ├óy l├Ā tiß║┐p tß╗źc ph├ón t├Łch vß╗øi MLE (kh├┤ng x├│a bß║źt kß╗│ mß╗źc n├Āo v├Ā c┼®ng kh├┤ng loß║Īi bß╗Å bß║źt kß╗│ quan s├Īt n├Āo) v├Ā x├Īc nhß║Łn lß║Īi kß║┐t quß║Ż ph├ón t├Łch th├┤ng qua Bootstrapping. Bootstrapping l├Ā qu├Ī tr├¼nh lß║źy mß║½u lß║Īi tr├¬n tß║Łp dß╗» liß╗ću hiß╗ćn c├│ bß║▒ng phŲ░ŲĪng ph├Īp lß║źy mß║½u vß╗øi thay thß║┐. Quy tr├¼nh thß╗æng k├¬ sß║Į t├Łnh to├Īn ─æß╗Ö lß╗ćch trung b├¼nh v├Ā chuß║®n cho mß╗Śi mß║½u c├│ k├Łch thŲ░ß╗øc N ─æß╗ā tß║Īo ra ph├ón phß╗æi lß║źy mß║½u mß╗øi.
T├Āi liß╗ću tham khß║Żo:
Collier, J. E. (2020). Applied structural
equation modeling using AMOS: Basic to advanced techniques. Routledge.
Hair, J. F., Anderson, R. E., Tatham, R. L., & Black, W. C. (2019).
Multivariate Data Analysis. In Cengage Learning (8th ed.). Cengage
Learning.




