MÃ HÃNH ÄO LÆŊáŧNG vs MÃ HÃNH CášĪU TRÃC
CÃC TIÃU CHÃ ÄÃNH GIÃ
Xin chà o cÃĄc anh cháŧ và cÃĄc bᚥn! CášĢm phiáŧn máŧi ngÆ°áŧi ghi rÃĩ nguáŧn amosleminh.com khi chia sášŧ hay sao chÃĐp náŧi dung táŧŦ website cáŧ§a chÚng tÃīi. TrÃĒn tráŧng cášĢm ÆĄn rášĨt nhiáŧu!
Trong bà i viášŋt nà y, chÚng ta sáš― tÃŽm hiáŧu
váŧ 2 khÃĄi niáŧm hay dÃđng trong cÃĄc bà i phÃĒn tÃch SEM, ÄÃģ là mÃī hÃŽnh Äo lÆ°áŧng vÃ
mÃī hÃŽnh cášĨu trÚc. NhÆ° vášy, thášŋ nà o là mÃī hÃŽnh Äo lÆ°áŧng? và thášŋ nà o là mÃī hÃŽnh cášĨu
trÚc? Sau ÄÃĒy, chÚng ta cÃđng Äi tÃŽm hiáŧu xem 2 loᚥi mÃī hÃŽnh nà y là nhÆ° thášŋ nà o.
MÃī hÃŽnh SEM bao gáŧm
hai loᚥi mÃī hÃŽnh là mÃī hÃŽnh cášĨu trÚc và mÃī hÃŽnh Äo lÆ°áŧng. Máŧi loᚥi mÃī hÃŽnh ÄÆ°áŧĢc
xÃĒy dáŧąng báŧi máŧt lÃ― thuyášŋt riÊng. MÃī hÃŽnh cášĨu trÚc ÄÆ°áŧĢc xÃĒy dáŧąng dáŧąa trÊn lÃ―
thuyášŋt náŧn (substantial theory), cÃēn mÃī hÃŽnh Äo lÆ°áŧng ÄÆ°áŧĢc hÃŽnh thà nh dáŧąa trÊn
lÃ― thuyášŋt háŧ tráŧĢ (auxiliary theory) (
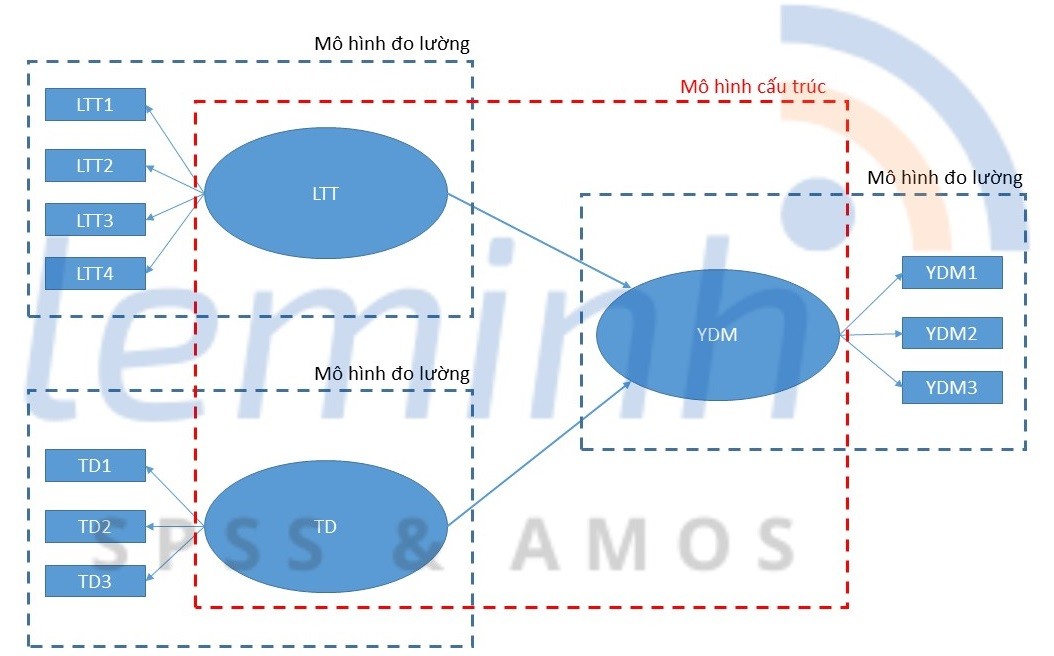
A. MÃī
hÃŽnh Äo lÆ°áŧng (measurement
model/outer model) là mÃī hÃŽnh tháŧ hiáŧn máŧi liÊn háŧ giáŧŊa khÃĄi niáŧm lÃ― thuyášŋt
(hay biášŋn cášĨu trÚc)1 và cÃĄc cháŧ bÃĄo (indicators) hay cÃĄc biášŋn quan sÃĄt
(observed variables). NhÆ° vášy trong mÃī hÃŽnh SEM sáš― cÃģ nhiáŧu mÃī hÃŽnh Äo lÆ°áŧng
cho cÃĄc khÃĄi niáŧm nghiÊn cáŧĐu khÃĄc nhau.
I. ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng
Äáŧi váŧi CB SEM sáŧ dáŧĨng AMOS, viáŧc ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng
chÃnh là ÄÃĄnh giÃĄ Äáŧ tin cášy, tÃnh háŧi táŧĨ và tÃnh phÃĒn biáŧt cáŧ§a thang Äo qua
phÆ°ÆĄng phÃĄp CFA. CÃĄc cháŧ tiÊu ÄÃĄnh giÃĄ cáŧĨ tháŧ cáŧ§a CFA chÚng tÃīi ÄÃĢ trÃŽnh bà y
nhiáŧu lᚧn áŧ cÃĄc chia sášŧ khÃĄc, trong cháŧ§ Äáŧ nà y chÚng tÃīi sáš― khÃīng thášĢo luášn lᚥi,
cÃĄc bᚥn cÃģ tháŧ tham khášĢo thÊm áŧ cÃĄc cháŧ§ Äáŧ cÅĐ hÆĄn.
CÃēn Äáŧi váŧi PLS SEM, viáŧc ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng ÄÆ°áŧĢc chia ra hai loᚥi: (1) ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng phášĢn ÃĄnh và (2) ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng cášĨu tᚥo.
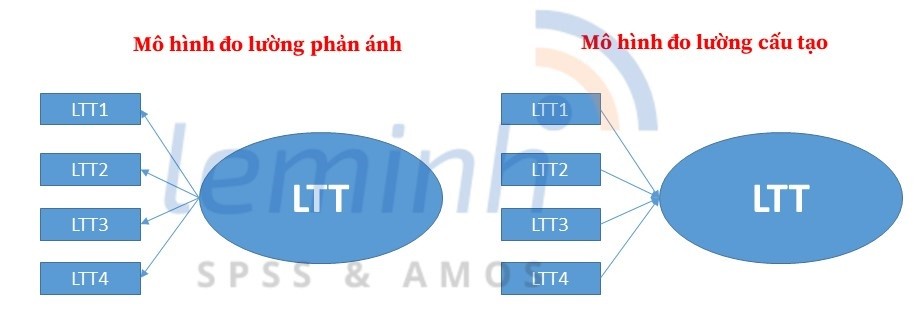
I.1. Äáŧi váŧi mÃī hÃŽnh Äo lÆ°áŧng phášĢn
ÃĄnh, chÚng ta cᚧn ÄÃĄnh giÃĄ 3 vášĨn Äáŧ sau ÄÃĒy:
âĒ
ÄÃĄnh giÃĄ máŧĐc Äáŧ tin cášy nhášĨt quÃĄn náŧi báŧ:
â Háŧ sáŧ tášĢi Outer loading âĨ 0.708. Trong máŧt và i trÆ°áŧng háŧĢp,
háŧ sáŧ tášĢi cÃģ tháŧ nháŧ hÆĄn 0.708. Trong trÆ°áŧng háŧĢp ÄÃģ, chÚng ta sáš― loᚥi báŧ cháŧ
bÃĄo ÄÃģ, nhÆ°ng cÅĐng cÃģ tháŧ xem xÃĐt giáŧŊ lᚥi (
â ÄÃĄnh giÃĄ máŧĐc Äáŧ tin cášy nhášĨt quÃĄn náŧi báŧ thÃīng qua háŧ sáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ tin cášy táŧng háŧĢp CR.
|
CR > 0.9 |
Máŧt sáŧ hoáš·c tášĨt cášĢ cÃĄc cháŧ bÃĄo cÃģ tháŧ Äang Äo lÆ°áŧng cÃđng
máŧt kášŋt quášĢ giáŧng nhau táŧŦ biášŋn tiáŧm ášĐn (cÃĄc cháŧ bÃĄo rášĨt giáŧng nhau váŧ máš·t Ã― nghÄĐa). Bᚥn cᚧn xem lᚥi máŧĐc Äáŧ chÃnh xÃĄc váŧ máš·t náŧi
dung và sau ÄÃģ loᚥi báŧ cháŧ bÃĄo và tháŧąc hiáŧn lᚥi phÃĒn tÃch. |
|
0.6 âĪ CR âĪ 0.7 |
ChášĨp nhášn ÄÆ°áŧĢc nášŋu dÃđng cho nghiÊn cáŧĐu khÃĄm phÃĄ. Nášŋu khÃīng cᚧn tÃŽm cÃĄch cášĢi thiáŧn CR và phÃĒn tÃch lᚥi mÃī
hÃŽnh PLS
SEM. |
|
CR < 0.6 |
KhÃīng chášĨp nhášn ÄÆ°áŧĢc. Cᚧn xem xÃĐt viáŧc xÃĒy dáŧąng lᚥi mÃī hÃŽnh Äo lÆ°áŧng hoáš·c thu thášp
thÊm dáŧŊ liáŧu sau ÄÃģ phÃĒn tÃch lᚥi mÃī hÃŽnh. |
âĒ ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ:
ÄÃĄnh giÃĄ máŧĐc Äáŧ tin cášy cáŧ§a táŧŦng cháŧ bÃĄo
|
l âĨ 0.7 |
Cháŧ bÃĄo Äᚥt máŧĐc Äáŧ
tin cášy |
|
0.4 âĪ l < 0.7 |
Cᚧn xem xÃĐt loᚥi báŧ
cháŧ bÃĄo và tháŧąc hiáŧn phÃĒn tÃch lᚥi mÃī hÃŽnh SEM |
|
l < 0.4 |
Loᚥi báŧ cháŧ bÃĄo vÃ
tháŧąc hiáŧn phÃĒn tÃch lᚥi. |
l là háŧ sáŧ tášĢi outer loading
ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ
|
AVE âĨ 0.5 |
Äᚥt ÄÆ°áŧĢc máŧĐc Äáŧ
chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ |
|
AVE < 0.5 |
KhÃīng Äᚥt máŧĐc Äáŧ
chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ. Cᚧn xem xÃĐt loᚥi báŧ cháŧ bÃĄo hoáš·c xem xÃĐt lᚥi viáŧc xÃĒy
dáŧąng mÃī hÃŽnh Äo lÆ°áŧng hoáš·c quÃĄ trÃŽnh thu thášp dáŧŊ liáŧu chÆ°a hiáŧu quášĢ. |
âĒ ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą phÃĒn biáŧt:
|
So sÃĄnh háŧ sáŧ tášĢi
ngoà i và háŧ sáŧ tášĢi chÃĐo (háŧ sáŧ tášĢi nášąm trÊn ÄÆ°áŧng chÃĐo) |
Cháŧ bÃĄo Äᚥt Äiáŧu kiáŧn cᚧn là háŧ sáŧ tášĢi ngoà i láŧn
hÆĄn háŧ sáŧ tášĢi chÃĐo. Trong trÆ°áŧng háŧĢp khÃīng Äᚥt Äiáŧu kiáŧn
cᚧn, chÚng ta cᚧn xem xÃĐt loᚥi báŧ cháŧ bÃĄo hoáš·c xÃĒy dáŧąng lᚥi mÃī hÃŽnh Äo lÆ°áŧng hoáš·c xem xÃĐt lᚥi hoᚥt Äáŧng thu thášp dáŧŊ liáŧu. |
|
HTMTij âĨ
0.9 |
KhÃģ Äᚥt ÄÆ°áŧĢc máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą phÃĒn biáŧt giáŧŊa cáš·p thang Äo i và j. Cᚧn xem xÃĐt loᚥi báŧ cháŧ bÃĄo hoáš·c xÃĒy dáŧąng lᚥi mÃī hÃŽnh Äo lÆ°áŧng
hoáš·c xem xÃĐt lᚥi hoᚥt Äáŧng thu thášp dáŧŊ liáŧu. |
|
HTMTij âĪ
0.85 |
Thang Äo Äᚥt ÄÆ°áŧĢc máŧĐc
Äáŧ chÃnh xÃĄc váŧ sáŧą phÃĒn biáŧt. |
I.2. Äáŧi váŧi mÃī hÃŽnh Äo lÆ°áŧng cášĨu
tᚥo, chÚng ta cᚧn ÄÃĄnh giÃĄ 3 vášĨn Äáŧ sau ÄÃĒy:
Äáŧi váŧi dᚥng mÃī hÃŽnh
Äo lÆ°áŧng nà y khÃĄ là Ãt gáš·p trong cÃĄc nghiÊn cáŧĐu. CÃĄc tiÊu chuášĐn kiáŧm Äáŧnh cho
mÃī hÃŽnh dᚥng nà y cÅĐng pháŧĐc tᚥp hÆĄn. Váŧ nguyÊn tášŊc thÃŽ chÚng ta sáš― cÃģ 3 tiÊu chà cᚧn ÄÃĄnh giÃĄ Äáŧi váŧi dᚥng mÃī hÃŽnh nà y. Tuy nhiÊn, nhiáŧu nghiÊn cáŧĐu khoa háŧc cháŧ Äáŧ cášp táŧi 2 tiÊu chà ÄÃĄnh giÃĄ là ÄÃĄnh giÃĄ váŧ háŧ sáŧ VIFs và máŧĐc Ã― nghÄĐa tháŧng kÊ cáŧ§a cÃĄc tráŧng sáŧ ngoà i (Outer weights), khÃīng cᚧn ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ. Trong chuyÊn Äáŧ nà y, chÚng tÃīi vášŦn Äáŧ cášp táŧi tiÊu chà ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ Äáŧ cÃĄc bᚥn nášŊm ÄÆ°áŧĢc káŧđ thuášt sÆĄ báŧ.
âĒ ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ:
Äáŧi váŧi dᚥng mÃī hÃŽnh Äo lÆ°áŧng cášĨu tᚥo (formative
measurement model) viáŧc ÄÃĄnh giÃĄ tÃnh chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ khÃĄ pháŧĐc tᚥp, báŧi
vÃŽ theo

BÆ°áŧc Äᚧu tiÊn, chÚng ta cᚧn tᚥo ra mÃī hÃŽnh ÄÆĄn cháŧ bÃĄo Äáŧ ÄÃĄnh giÃĄ mÃī hÃŽnh Äo lÆ°áŧng cho YDM.
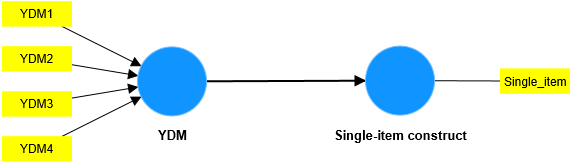
Kiáŧm tra giÃĄ tráŧ háŧi qui cáŧ§a ÄÆ°áŧng dášŦn láŧn hÆĄn hoáš·c bášąng 0.7 (và P value cÃģ Ã― nghÄĐa tháŧng kÊ) hay RÂē âĨ 0.5 thÃŽ kášŋt luášn mÃī hÃŽnh Äo lÆ°áŧng cášĨu tᚥo ÄášĢm bášĢo Äáŧ chÃnh xÃĄc váŧ tÃnh háŧi táŧĨ. Kášŋt quášĢ phÃĒn tÃch tÃŽnh huáŧng tháŧąc tášŋ cho thášĨy, mÃī hÃŽnh Äo lÆ°áŧng YDM ÄášĢm bášĢo Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ.
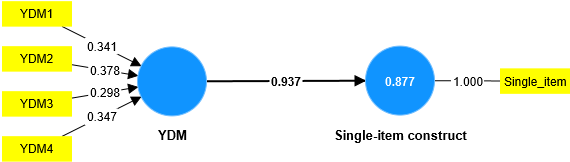
VášĨn Äáŧ pháŧĐc tᚥp và khÃģ khÄn nhášĨt cáŧ§a chÚng ta áŧ tiÊu chà ÄÃĄnh giÃĄ nà y là káŧđ thuášt tᚥo ra biášŋn Single-item construct nhÆ° chÚng ta thášĨy áŧ trÊn. Máš·c dÃđ Hair và cáŧng sáŧą (2021) cÃģ Äáŧ cášp táŧi, nhÆ°ng cÅĐng cháŧ dáŧŦng lᚥi áŧ máŧĐc giáŧi thiáŧu phÆ°ÆĄng phÃĄp. Thay và o ÄÃģ, tÃĄc giášĢ giáŧi thiáŧu phÆ°ÆĄng phÃĄp 3 bÆ°áŧc cáŧ§a Cheah và cáŧng sáŧą (2018), chi tiášŋt nhÆ° sau (chÚng tÃīi xin phÃĐp ÄÆ°áŧĢc trÃŽnh bà y vÄn bášĢn gáŧc trÃch tᚥi EXHIBIT 5.3 trang 144 cáŧ§a cuáŧn A primer on partial least squares structural equation modeling (PLS-SEM)):
 Cheah et al. (2018) have proposed the following three-step
procedure for generating and validating global single items to be used as
criterion variables in a redundancy analysis. Their procedure requires
empirical data to be collected as part of a pilot study to validate the single
item.
Cheah et al. (2018) have proposed the following three-step
procedure for generating and validating global single items to be used as
criterion variables in a redundancy analysis. Their procedure requires
empirical data to be collected as part of a pilot study to validate the single
item.
Step 1: Item generation
To generate a suitable single item, researchers need to carefully
choose a theoretical definition of the concept of interest and identify popular
measurement scales that build on this definition. Taking the scale items as
input, researchers then need to create a measure that taps the most relevant
aspect of the concept and the scale items. The resulting item should be checked
for face validity by a panel of experts and members representing the target
population.
Step 2: Reliability assessment
To assess the single itemâs reliability, researchers can draw on
the following formula:
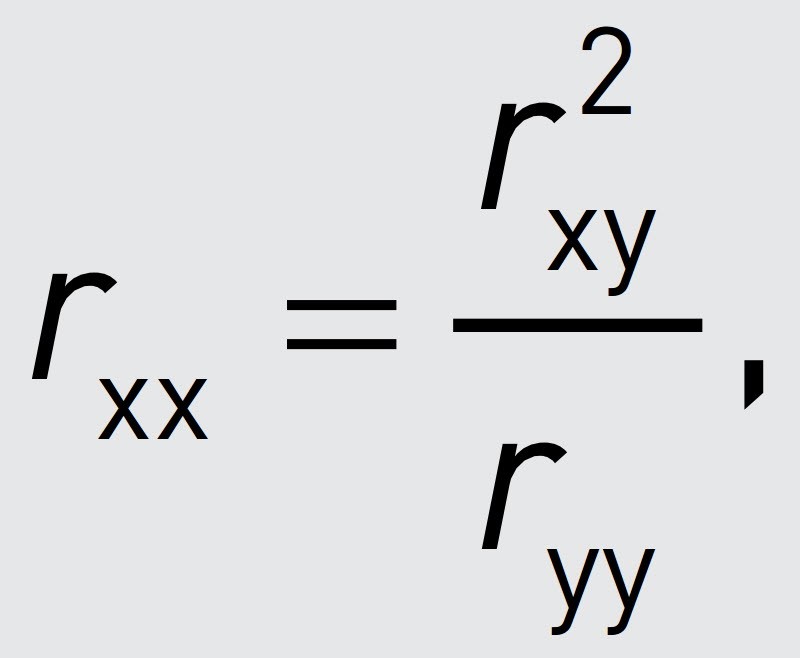
where rxx is the reliability estimate of the single-item
measure x, ryy is the reliability of the reflective multi-item
measure of the same concept (e.g., as depicted by ÏA; Chapter 4),
and rxy is the correlation between the single-item and multi-item measure
of the same concept. Hence, reliability assessment by means of this formula
requires the simultaneous administration of a single-item and a multi-item measure
of the same concept, for example, as part of a pilot study. The internal consistency
reliability should be 0.7 or higher.
Step 3: Convergent and criterion validity assessment
 Biášŋn Single-item ÄÆ°áŧĢc tᚥo ra theo cÃĄch xÃĒy dáŧąng máŧt thang Äo táŧng quÃĄt bášąng máŧt cÃĒu háŧi duy nhášĨt (item), và dáŧĨ à Äáŧnh mua ÄÆ°áŧĢc xÃĒy dáŧąng bášąng máŧt cÃĒu háŧi nhÆ°: NhÃŽn chung, tÃīi muáŧn mua sášĢn phášĐm/dáŧch váŧĨ nà y? LÆ°u Ã― rášąng, thang Äo cáŧ§a biášŋn Single-item và thang Äo cáŧ§a YDM phášĢi cÃģ cÃđng dᚥng và tÆ°ÆĄng Äáŧng váŧ kÃch thÆ°áŧc (chášģng hᚥn nhÆ° bᚥn sáŧ dáŧĨng likert 5 Äiáŧm Äáŧ Äo lÆ°áŧng YDM thÃŽ Single-item cÅĐng phášĢi dÃđng likert 5 Äiáŧm).
Biášŋn Single-item ÄÆ°áŧĢc tᚥo ra theo cÃĄch xÃĒy dáŧąng máŧt thang Äo táŧng quÃĄt bášąng máŧt cÃĒu háŧi duy nhášĨt (item), và dáŧĨ à Äáŧnh mua ÄÆ°áŧĢc xÃĒy dáŧąng bášąng máŧt cÃĒu háŧi nhÆ°: NhÃŽn chung, tÃīi muáŧn mua sášĢn phášĐm/dáŧch váŧĨ nà y? LÆ°u Ã― rášąng, thang Äo cáŧ§a biášŋn Single-item và thang Äo cáŧ§a YDM phášĢi cÃģ cÃđng dᚥng và tÆ°ÆĄng Äáŧng váŧ kÃch thÆ°áŧc (chášģng hᚥn nhÆ° bᚥn sáŧ dáŧĨng likert 5 Äiáŧm Äáŧ Äo lÆ°áŧng YDM thÃŽ Single-item cÅĐng phášĢi dÃđng likert 5 Äiáŧm).
NhÃŽn chung, viáŧc tᚥo ra máŧt biášŋn Single-item trong trÆ°áŧng háŧĢp nà y là khÃīng phášĢi ÄÆĄn giášĢn, báŧi láš― cÃĒu háŧi chung nášŋu khÃīng ÄÆ°áŧĢc nghiÊn cáŧĐu káŧđ sáš― tᚥo ra kášŋt quášĢ sai láŧch, táŧŦ ÄÃģ là m ášĢnh hÆ°áŧng Äášŋn vášĨn Äáŧ kiáŧm Äáŧnh thang Äo. ChÃnh vÃŽ sáŧą khÃģ khÄn, pháŧĐc tᚥp và táŧn kÃĐm chi phà trong vášĨn Äáŧ tᚥo ra biášŋn Single-item mà hiáŧn nay, cÃĄc nghiÊn cáŧĐu khoa háŧc thÆ°áŧng báŧ qua tiÊu chà ÄÃĄnh giÃĄ nà y Äáŧi váŧi mÃī hÃŽnh formative. ÄÃĒy là cÃĄc video hÆ°áŧng dášŦn cáŧ§a cÃĄc chuyÊn gia sáŧ liáŧu trÊn thášŋ giáŧi, cÃĄc bᚥn cÃģ tháŧ tham khášĢo thÊm tᚥi ÄÃĒy: video 1; video 2; v.v.
âĨ LÆ°u Ã― rášąng, khi Äášŋn váŧi Dáŧch váŧĨ sáŧ liáŧu LÊ Minh, khi cÃĄc anh cháŧ cÃģ nhu cᚧu ÄÃĄnh giÃĄ tiÊu chà nà y, chÚng tÃīi sášĩn sà ng háŧ tráŧĢ và hÆ°áŧng dášŦn cÃĄc anh cháŧ chi tiášŋt cÃĄch tháŧĐc tᚥo ra single item Äáŧ ÄášĢm bášĢo tiÊu chà ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ sáŧą háŧi táŧĨ Äᚥt yÊu cᚧu.
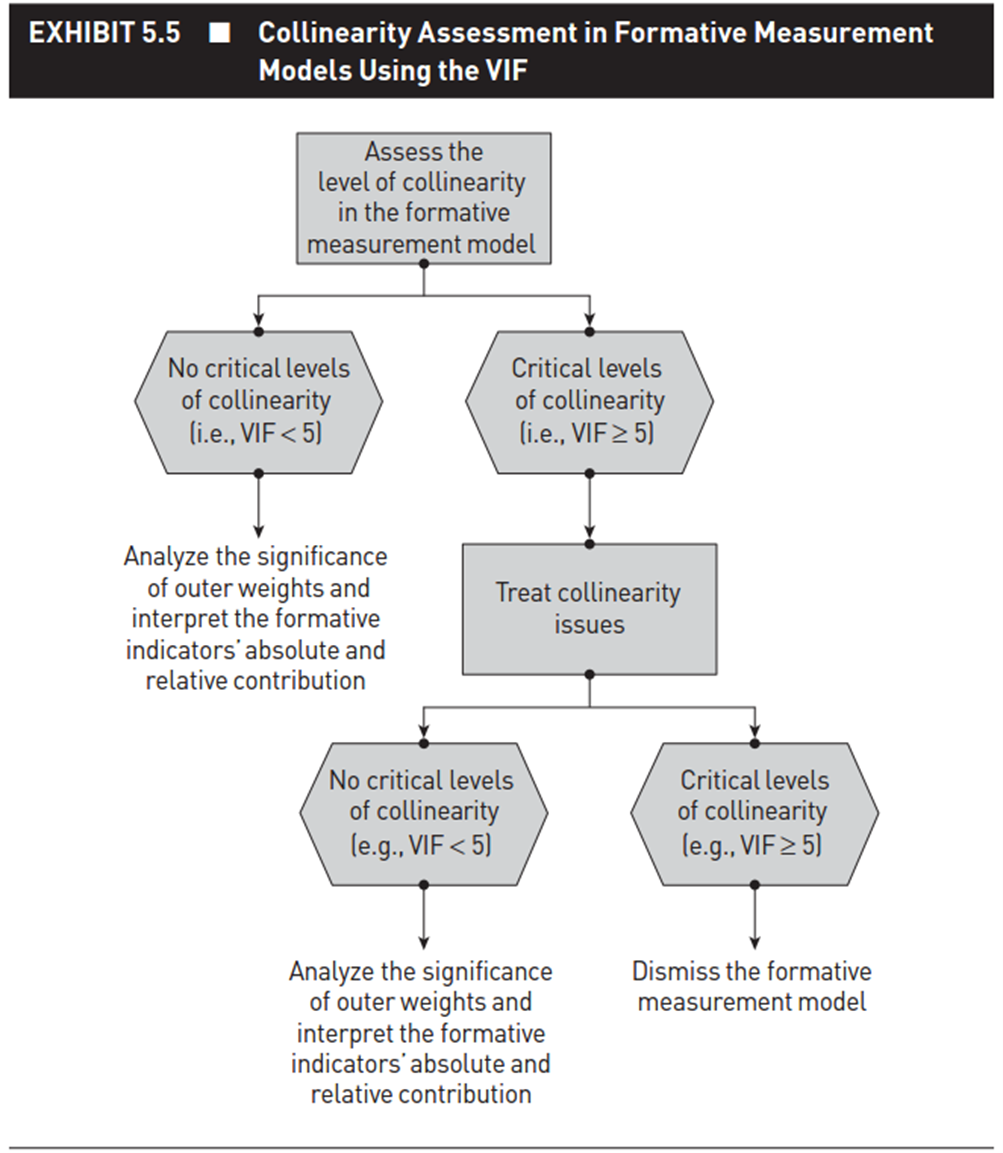
Viáŧc ÄÃĄnh giÃĄ máŧĐc Äáŧ Äa cáŧng tuyášŋn cáŧ§a mÃī hÃŽnh Äo lÆ°áŧng cášĨu tᚥo cᚧn ÄÆ°áŧĢc xem xÃĐt trÊn mÃī hÃŽnh ÄÆĄn cháŧ bÃĄo ÄÃĢ ÄÆ°áŧĢc tᚥo lášp. Theo Hair và cáŧng sáŧą (2021), nášŋu VIF < 5 thÃŽ kášŋt luášn cÃĄc cháŧ bÃĄo khÃīng gáš·p hiáŧn tÆ°áŧĢng Äa cáŧng tuyášŋn. Trong máŧt và i trÆ°áŧng háŧĢp VIF âĨ 5, chÚng ta cᚧn xem xÃĐt loᚥi báŧ cÃĄc cháŧ bÃĄo cÃģ VIF âĨ 5. LÆ°u Ã― rášąng, do Äáš·c thÃđ lÃ― thuyášŋt cáŧ§a mÃī hÃŽnh formative, nÊn viáŧc loᚥi báŧ cháŧ bÃĄo là khÃīng nÊn vÃŽ nhÆ° thášŋ sáš― ášĢnh hÆ°áŧng Äášŋn chášĨt lÆ°áŧĢng construct. Bᚥn nÊn xem xÃĐt lᚥi toà n báŧ quÃĄ trÃŽnh xÃĒy dáŧąng mÃī hÃŽnh và quÃĄ trÃŽnh tháŧąc hiáŧn khášĢo sÃĄt ÄášĢm bášĢo tÃnh chuášĐn cáŧ§a dáŧŊ liáŧu Äᚧu và o.

Kášŋt quášĢ phÃĒn tÃch mÃī hÃŽnh tháŧąc hà nh cho thášĨy, cÃĄc cháŧ bÃĄo ÄášĢm bášĢo tÃnh Äa cáŧng tuyášŋn.
SÆĄ Äáŧ biáŧu diáŧ n quÃĄ trÃŽnh kiáŧm tra VIF cho mÃī hÃŽnh formative (nguáŧn Hair và cáŧng sáŧą (2021)):
âĒ ÄÃĄnh giÃĄ máŧĐc Ã― nghÄĐa tháŧng kÊ cáŧ§a giÃĄ
tráŧ tráŧng sáŧ ngoà i (sáŧ dáŧĨng phÆ°ÆĄng phÃĄp bootstrap):
LÆ°u Ã―, bÆ°áŧc ÄÃĄnh giÃĄ nà y chÚng ta sáš― tháŧąc hiáŧn trÊn mÃī hÃŽnh chÃnh. Chᚥy bootstrap (váŧi N Äáŧ ngháŧ là 5000). ChÚng ta ÄÃĄnh giÃĄ Pvalue cáŧ§a cÃĄc tráŧng sáŧ ngoà i. Nášŋu P value nháŧ hÆĄn 5%, kášŋt luášn tráŧng sáŧ khÃĄc giÃĄ tráŧ 0 cÃģ Ã― nghÄĐa tháŧng kÊ, mÃī hÃŽnh Äo lÆ°áŧng cášĨu tᚥo Äᚥt yÊu cᚧu.
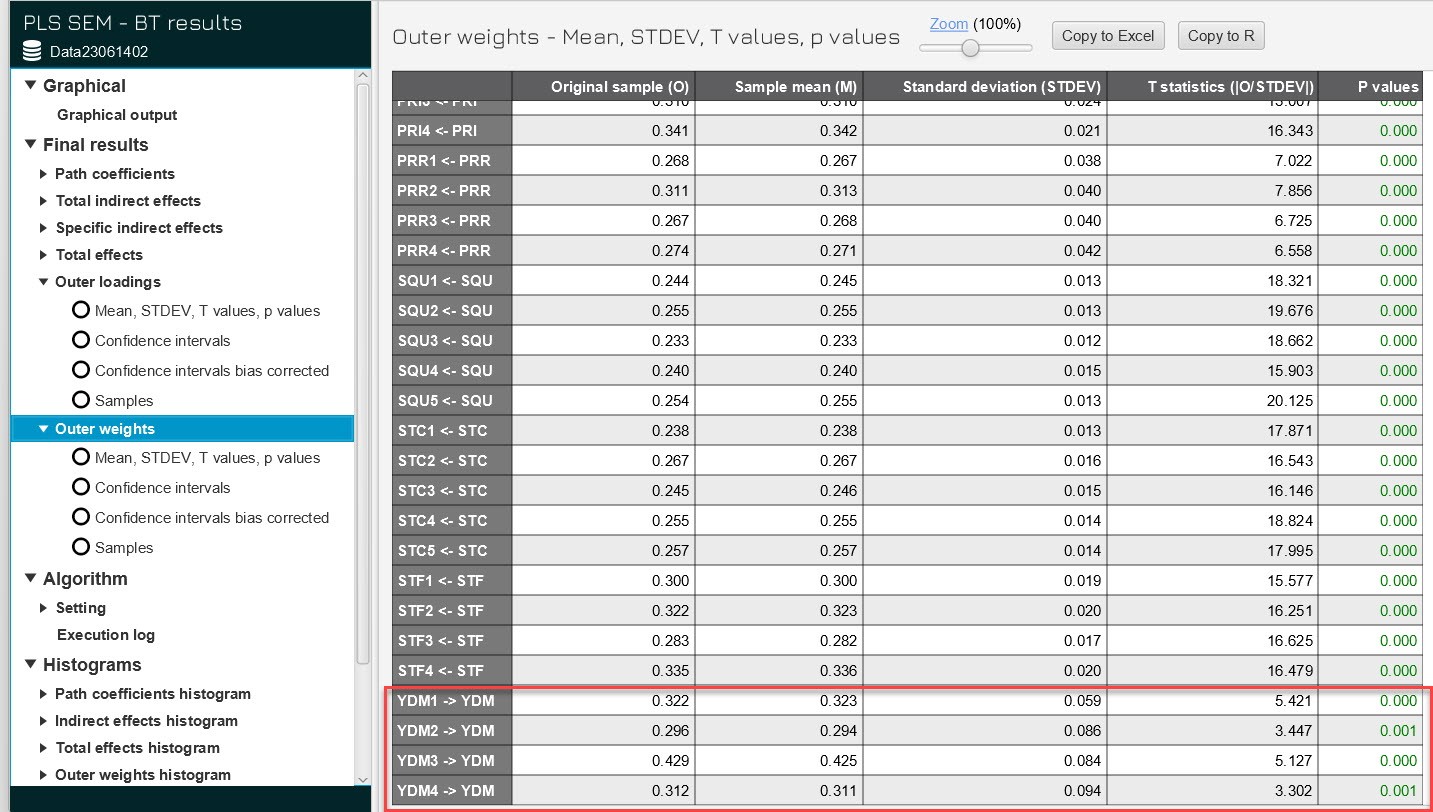
Trong nhiáŧu trÆ°áŧng háŧĢp nášŋu P value cáŧ§a tráŧng sáŧ ngoà i (outer weights) khÃīng Äᚥt máŧĐc Ã― nghÄĐa tháŧng kÊ (>5%) thÃŽ khoan váŧi loᚥi biášŋn, chÚng ta cᚧn tiášŋp táŧĨc ÄÃĄnh giÃĄ máŧĐc Ã― nghÄĐa tháŧng kÊ cáŧ§a háŧ sáŧ outer loading cáŧ§a cÃĄc cháŧ bÃĄo áŧ mÃī hÃŽnh formative. Nášŋu háŧ sáŧ tášĢi tráŧng ngoà i cáŧ§a cÃĄc cháŧ bÃĄo cáŧ§a mÃī hÃŽnh formative âĨ 5 thÃŽ cÃĄc cháŧ bÃĄo vášŦn ÄÆ°áŧĢc giáŧŊ lᚥi trong mÃī hÃŽnh máš·c dÃđ nÃģ khÃīng cÃģ Ã― nghÄĐa. Trong trÆ°áŧng háŧĢp háŧ sáŧ tášĢi tráŧng ngoà i < 5 thÃŽ cᚧn ÄÃĄnh giÃĄ thÊm máŧĐc Ã― nghÄĐa tháŧng kÊ cáŧ§a nÃģ. Nášŋu máŧĐc Ã― nghÄĐa tháŧng kÊ Äᚥt yÊu cᚧu thÃŽ xem xÃĐt cÃģ nÊn loᚥi cháŧ bÃĄo ÄÃģ ra kháŧi mÃī hÃŽnh formative hay khÃīng (lÆ°u Ã― rášąng, viáŧc loᚥi nà y cᚧn cÃĒn nhášŊc thášt káŧđ lÆ°áŧng vÃŽ bášĢn chášĨt cáŧ§a loᚥi mÃī hÃŽnh formative), nášŋu máŧĐc Ã― nghÄĐa tháŧng kÊ khÃīng Äᚥt yÊu cᚧu thÃŽ loᚥi biášŋn ÄÃģ ra kháŧi mÃī hÃŽnh formative. Sau ÄÃĒy là lÆ°u Äáŧ kiáŧm tra háŧ sáŧ outer weights ÄÆ°áŧĢc trÃch dášŦn táŧŦ Hair và cáŧng sáŧą (2021).
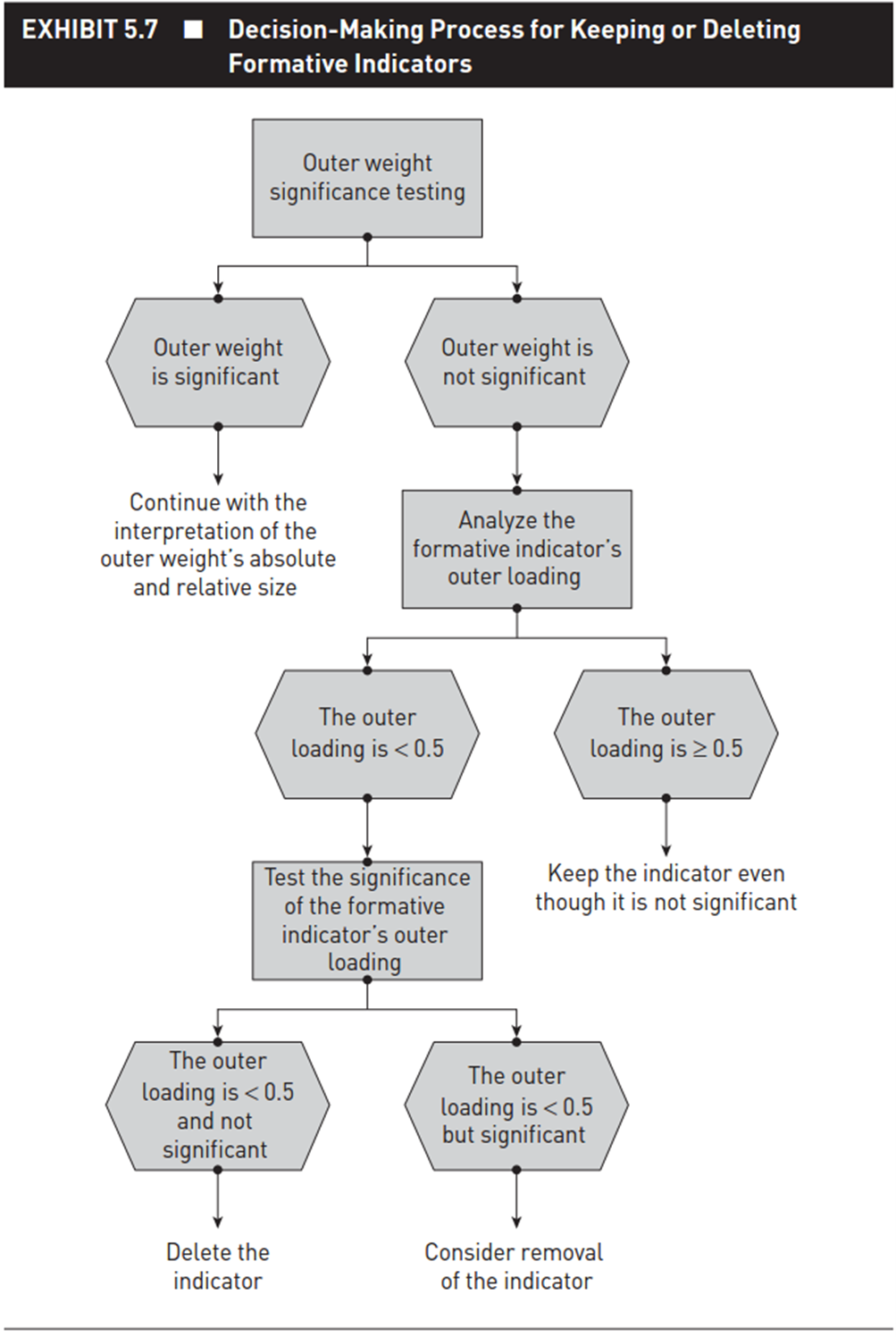
NhÆ° vášy, táŧi ÄÃĒy chÚng ta ÄÃĢ kášŋt thÚc ÄÆ°áŧĢc viáŧc ÄÃĄnh giÃĄ mÃī
hÃŽnh Äo lÆ°áŧng. Tiášŋp theo, chÚng ta sáš― xem xÃĐt ÄÃĄnh giÃĄ mÃī hÃŽnh cášĨu trÚc.
B. MÃī
hÃŽnh cášĨu trÚc (structural model/ inner model) là mÃī hÃŽnh tháŧ hiáŧn cÃĄc máŧi liÊn háŧ
giáŧŊa cÃĄc khÃĄi niáŧm nghiÊn cáŧĐu trong mÃī hÃŽnh SEM. NhÆ° vášy, máŧt mÃī hÃŽnh SEM cháŧ
cÃģ máŧt mÃī hÃŽnh cášĨu trÚc. Viáŧc ÄÃĄnh giÃĄ mÃī hÃŽnh cášĨu trÚc SEM, áŧ ÄÃĒy, chÚng tÃīi
chia ra là m hai loᚥi: máŧt là mÃī hÃŽnh CB SEM, hai là mÃī hÃŽnh PLS SEM.
I.1. Äáŧi váŧi mÃī hÃŽnh CB SEM, viáŧc chᚥy mÃī hÃŽnh bášąng AMOS rášĨt
quen thuáŧc váŧi chÚng ta. ÄÃĄnh giÃĄ mÃī hÃŽnh cášĨu trÚc CB SEM cÃĄc bᚥn tháŧąc hiáŧn tháŧ§
táŧĨc ÄÃĄnh giÃĄ mÃī hÃŽnh SEM chᚥy AMOS nhÆ° chÚng tÃīi ÄÃĢ trÃŽnh bà y áŧ trong cÃĄc chuyÊn
Äáŧ cÅĐ hÆĄn.
I.2. Äáŧi váŧi mÃī hÃŽnh PLS SEM, viáŧc ÄÃĄnh giÃĄ mÃī hÃŽnh cášĨu trÚc ÄÆ°áŧĢc
tháŧąc hiáŧn nhÆ° sau:

âĒ ÄÃĄnh giÃĄ máŧĐc Äáŧ Äa cáŧng tuyášŋn
giáŧŊa cÃĄc biášŋn giášĢi thÃch trong máŧt mÃī hÃŽnh SEM. LÆ°u Ã―, chÚng ta xem xÃĐt VIF áŧ máŧĨc Inner model
trong thuášt toÃĄn chᚥy PLS SEM táŧŦ SmartPLS. Nášŋu VIF âĪ 5 thÃŽ kášŋt luášn, khÃīng xuášĨt
hiáŧn hiáŧn tÆ°áŧĢng Äa cáŧng tuyášŋn. Nášŋu táŧi ÄÃĒy, VIF > 5 thÃŽ cháŧ cÃēn con ÄÆ°áŧng
duy nhášĨt là bᚥn phášĢi xem xÃĐt lᚥi toà n báŧ lÃ― thuyášŋt Äᚧu và o và khášĢo sÃĄt lᚥi sáŧ
liáŧu.
âĒ ÄÃĄnh giÃĄ máŧĐc Ã― nghÄĐa tháŧng kÊ và kášŋt luášn cÃĄc giášĢ
thuyášŋt nghiÊn cáŧĐu.
âĒ ÄÃĄnh giÃĄ vai trÃē giášĢi thÃch cáŧ§a biášŋn Äᚧu táŧi biášŋn pháŧĨ thuáŧc thÃīng qua háŧ sáŧ RÂē, RÂē hiáŧu cháŧnh, và cháŧ sáŧ fÂē. Chi tiášŋt ÄÃĄnh giÃĄ bᚥn cÃģ tháŧ tham khášĢo áŧ cÃĄc chuyÊn Äáŧ cÅĐ hÆĄn cáŧ§a chÚng tÃīi.
âĒ ÄÃĄnh giÃĄ máŧĐc Äáŧ chÃnh xÃĄc váŧ dáŧą bÃĄo thÃīng qua cÃĄc háŧ sáŧ QÂē và ÄÃĄnh giÃĄ hiáŧu quášĢ dáŧą bÃĄo cáŧ§a máŧt biášŋn giášĢi thÃch thÃīng qua biáŧu Äáŧ phÃĒn tÃch IP, sáŧ dáŧĨng phÆ°ÆĄng phÃĄp IPMA (chÚng tÃīi ÄÃĢ trÃŽnh bà y chi tiášŋt áŧ trong máŧt chuyÊn Äáŧ cÅĐ hÆĄn).
Táŧi ÄÃĒy, chÚng ta ÄÃĢ kášŋt thÚc xong phᚧn ÄÃĄnh giÃĄ mÃī
hÃŽnh cášĨu trÚc. NhÆ° vášy, khi kiáŧm tra mÃī hÃŽnh PLS SEM, chÚng ta sáš― ÄÃĄnh giÃĄ áŧ cášĢ
hai mÃī hÃŽnh là mÃī hÃŽnh Äo lÆ°áŧng và mÃī hÃŽnh cášĨu tᚥo.
 1. Bᚥn Äáŧc cᚧn phÃĒn biáŧt
giáŧŊa khÃĄi niáŧm lÃ― thuyášŋt và biášŋn cášĨu trÚc. KhÃĄi niáŧm lÃ― thuyášŋt ÄÆ°áŧĢc Äo lÆ°áŧng báŧi
máŧt trong ba loᚥi biášŋn cášĨu trÚc. Theo
1. Bᚥn Äáŧc cᚧn phÃĒn biáŧt
giáŧŊa khÃĄi niáŧm lÃ― thuyášŋt và biášŋn cášĨu trÚc. KhÃĄi niáŧm lÃ― thuyášŋt ÄÆ°áŧĢc Äo lÆ°áŧng báŧi
máŧt trong ba loᚥi biášŋn cášĨu trÚc. Theo
TÃ i liáŧu tham khášĢo
Hair Jr, J. F., Hult,
G. T. M., Ringle, C. M., & Sarstedt, M. (2021). A primer on partial
least squares structural equation modeling (PLS-SEM). Sage publications.
Henseler, J., &
Schuberth, F. (2020). Using confirmatory composite analysis to assess emergent
variables in business research. Journal of Business Research, 120,
147â156.
Hulland, J. (1999).
Use of partial least squares (PLS) in strategic management research: A review
of four recent studies. Strategic Management Journal, 20(2), 195â204.
VÅĐ HáŧŊu Thà nh, & Nguyáŧ n Minh Hà . (2023). GiÃĄo trÃŽnh phÃĒn tÃch dáŧŊ liáŧu ÃĄp dáŧĨng mÃī hÃŽnh PLS - SEM (1st ed.). NXB ÄH Quáŧc Gia Tp HCM.
Sarstedt, M., Hair Jr,
J. F., Cheah, J. H., Becker, J. M., & Ringle, C. M. (2019). How to specify,
estimate, and validate higher-order constructs in PLS-SEM. Australasian marketing journal, 27(3), 197-211.




