CÃC CHáŧ Sáŧ DÃNG Äáŧ ÄO LÆŊáŧNG TRONG MÃ HÃNH PLS SEM
1. Cháŧ sáŧ GoF (Goodness
of fit)
Trong mÃī hÃŽnh PLS SEM cÃģ máŧt cháŧ sáŧ Äáŧ Äo lÆ°áŧng Äáŧ phÃđ háŧĢp cáŧ§a mÃī hÃŽnh ÄÆ°áŧĢc gáŧi là Goodness of fit - GoF. GoF ÄÆ°áŧĢc Tenenhaus và cáŧng sáŧą ÄÆ°a ra và o nÄm 2004 Äáŧ Äo lÆ°áŧng mÃī hÃŽnh ÄÆ°áŧng dášŦn PLS (Partial least squares). Cháŧ sáŧ GoF cÃģ giÃĄ tráŧ nášąm trong Äoᚥn táŧŦ 0 Äášŋn 1, cà ng gᚧn 1 thÃŽ mÃī hÃŽnh cà ng phÃđ háŧĢp táŧt. Giáŧ mÃŽnh sáš― tÃnh cháŧ sáŧ nà y dáŧąa trÊn mÃī hÃŽnh minh háŧa bÊn dÆ°áŧi.
Sau khi chᚥy xong mÃī hÃŽnh, bᚥn cᚧn trÃch xuášĨt dáŧŊ liáŧu
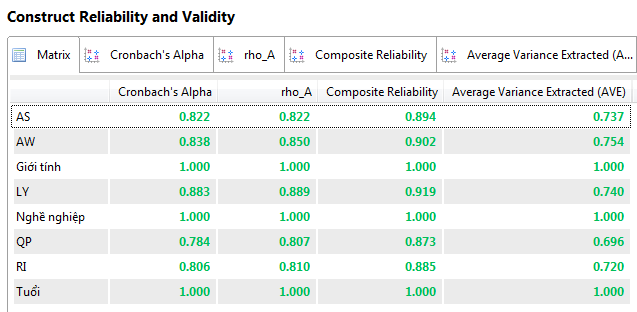
Cháŧ sáŧ GoF ÄÆ°áŧĢc tÃnh bášąng cÃīng tháŧĐc:
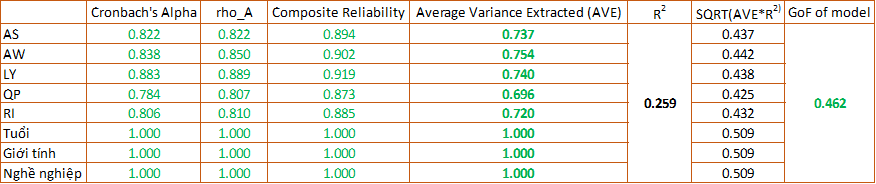
NhÆ° vášy chÚng ta ÄÃĢ tÃnh ÄÆ°áŧĢc máŧt trong nháŧŊng cháŧ sáŧ Äo lÆ°áŧng Äáŧ Äáŧ phÃđ háŧĢp cáŧ§a mÃī hÃŽnh PLS SEM. GiÃĄ tráŧ GoF là 0.462 ÄÆ°áŧĢc ÄÃĄnh giÃĄ là mÃī hÃŽnh cÃģ Äáŧ phÃđ háŧĢp láŧn váŧi báŧ dáŧŊ liáŧu nghiÊn cáŧĐu, máŧĐc Äáŧ mᚥnh yášŋu ÄÆ°áŧĢc ÄÃĄnh giÃĄ theo cÆĄ sáŧ cáŧ§a Wetzels và cáŧng sáŧą (2009).
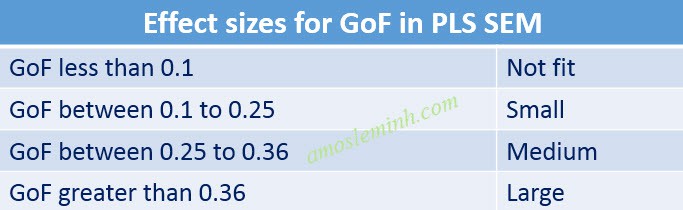
2. Cháŧ sáŧ Q2 (Predictive Relevance)
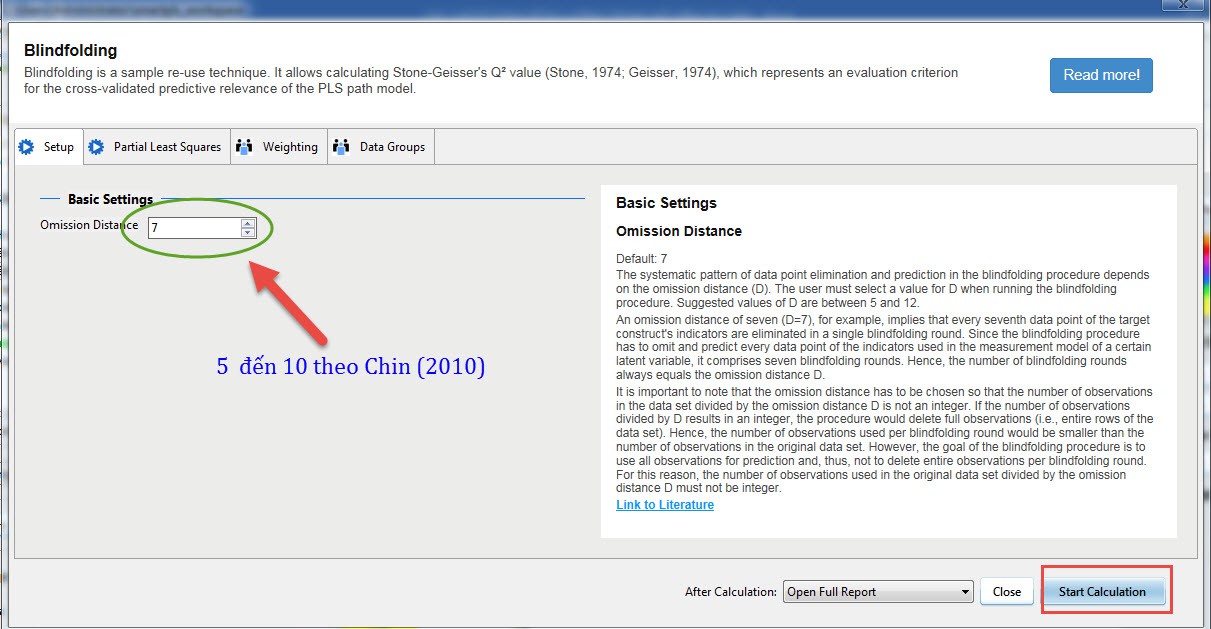
Cháŧ sáŧ Q2 là kášŋt quášĢ khi bᚥn chᚥy tháŧ§ táŧĨc Blindfolding,
nÃģ dáŧą ÄoÃĄn xem mÃī hÃŽnh nghiÊn cáŧĐu cÃģ phÃđ háŧĢp hay khÃīng. Khi chᚥy tháŧ§ táŧĨc Blindfolding
sáš― cÃģ 2 bášĢng kášŋt quášĢ cháŧĐa Q2, tháŧĐ nhášĨt là Cross Validated redundancy,
tháŧĐ hai là Cross validated communality. ChÚng ta cháŧ quan tÃĒm Äášŋn kášŋt quášĢ táŧŦ bášĢng
tháŧĐ nhášĨt Cross Validated redundancy. Theo Fornell and Cha (1994), giÃĄ tráŧ Q2
> 0 thÃŽ mÃī hÃŽnh ÄÆ°áŧĢc ÄÃĄnh giÃĄ là phÃđ háŧĢp táŧt, và ngÆ°áŧĢc lᚥi mÃī hÃŽnh ÄÆ°áŧĢc dáŧą
ÄoÃĄn là thiášŋu Äáŧ phÃđ háŧĢp.
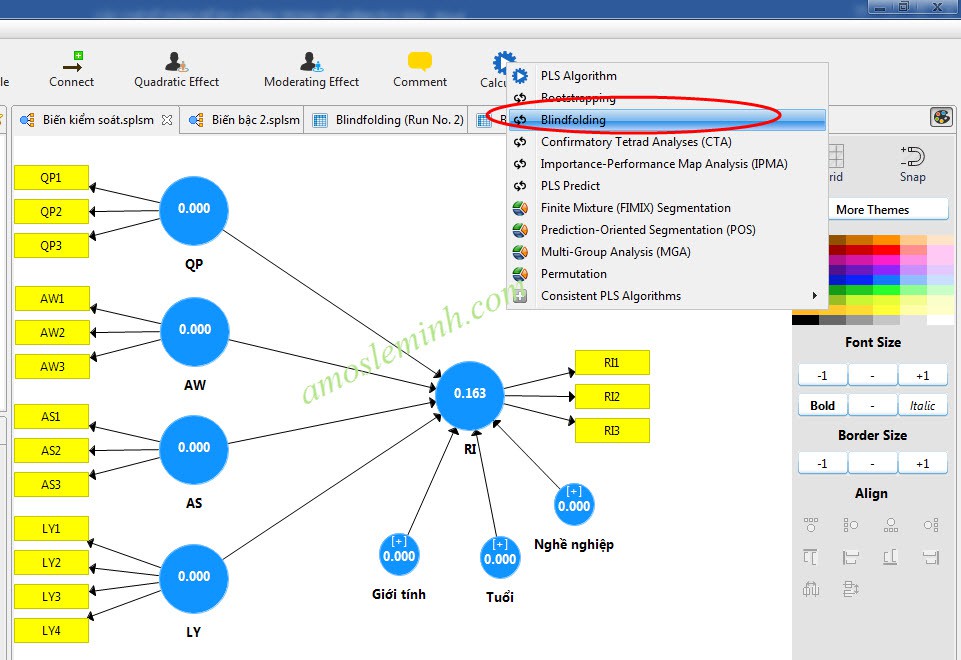
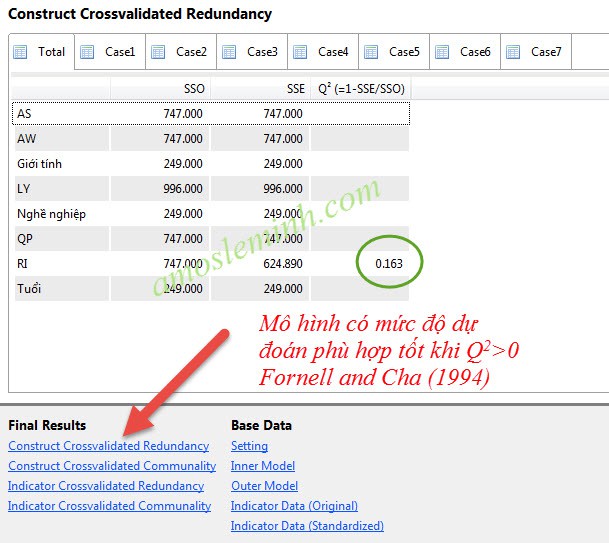
Kášŋt quášĢ phÃĒn tÃch và dáŧĨ xuášĨt ra táŧŦ SmartPLS nhÆ° trÊn ÄÃĢ cho thášĨy mÃī hÃŽnh ÄÆ°áŧĢc tiÊn ÄoÃĄn là phÃđ háŧĢp táŧt.
3. Cháŧ sáŧ f2 (Predictive Relevance)
Chin (1998) cho biášŋt rášąng, máŧĐc Äáŧ ášĢnh hÆ°áŧng tÆ°ÆĄng Äáŧi cáŧ§a máŧt biášŋn
tiáŧm ášĐn ngoᚥi sinh (particular exogenous latent variable) lÊn cÃĄc biášŋn tiáŧm ášĐn
náŧi sinh (endogenous latent variables) bášąng sáŧą thay Äáŧi cáŧ§a R2. Cháŧ
sáŧ f2 ÄÆ°áŧĢc tÃnh bášąng sáŧą gia tÄng R2 cáŧ§a biášŋn tiáŧm ášĐn cÃģ ÄÆ°áŧng
dášŦn ÄuáŧĢc kášŋt náŧi, hay nÃģi cÃĄch khÃĄc f2 ÄÆ°áŧĢc tÃnh theo táŧŦng cáš·p tÆ°ÆĄng
quan cáŧĨ tháŧ.
Cháŧ sáŧ f2 ÄÆ°áŧĢc tÃnh theo cÃīng tháŧĐc sau:
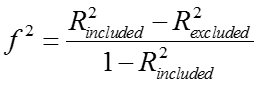
MáŧĐc Äáŧ ášĢnh hÆ°áŧng ÄÆ°áŧĢc ÄÃĄnh giÃĄ nhÆ° sau:
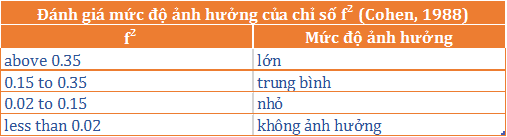
Kášŋt quášĢ táŧŦ và dáŧĨ ban Äᚧu:
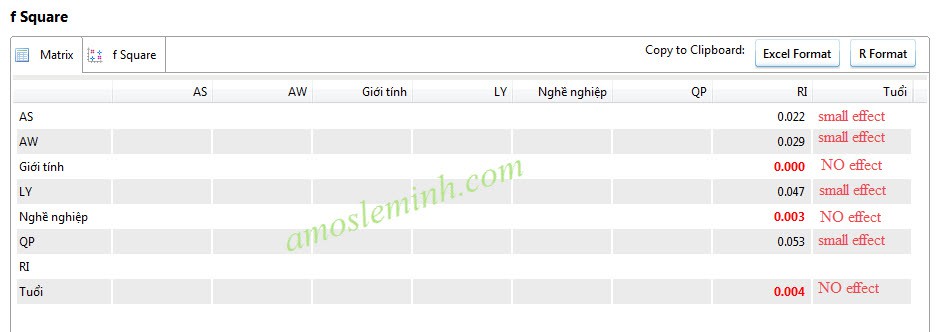
TrÃch táŧŦ Henseler, Ringle & Sinkovics (2009)

TÃ i liáŧu tham khášĢo
Chin, W. W. (1998). The partial least squares approach to
structural equation modeling. Modern Methods for Business Research, 295(2),
295â336.
Chin, W. W. (2010). How to write up and report PLS analyses.
In Handbook of partial least squares (pp. 655â690). Springer.
Fornell, C., & Cha, J. (1994). Partial Least Squares. Advanced Methods of Marketing Research, RP Bagozzi. Cambridge, Blackwell.
Henseler, J., Ringle, C. M., & Sinkovics, R. R. (2009). The use of partial least squares path modeling in international marketing. In New challenges to international marketing. Emerald Group Publishing Limited.
Tenenhaus, M., Amato, S., & Esposito Vinzi, V. (2004). A
global goodness-of-fit index for PLS structural equation modelling. In Proceedings
of the XLII SIS scientific meeting (Vol. 1, pp. 739â742).
Wetzels, M., Odekerken-SchrÃķder, G., & Van Oppen, C. (2009). Using PLS path modeling for assessing hierarchical construct models: Guidelines and empirical illustration. MIS Quarterly, 177â195.




