KIáŧM ÄáŧNH ÆŊáŧC LÆŊáŧĒNG HáŧI QUI
BIášūN TRUNG GIAN TRONG MÃ HÃNH CB SEM (PHášĶN 1)

Kášŋt thÚc bÆ°áŧc phÃĒn tÃch mÃī hÃŽnh SEM, váŧ cÆĄ bášĢn chÚng ta ÄÃĢ
hoà n thà nh, tuy nhiÊn Äáŧ biášŋt ÄÆ°áŧĢc cÃĄc Æ°áŧc lÆ°áŧĢng (tráŧng sáŧ háŧi qui) ÄÆ°áŧĢc trÃch xuášĨt táŧŦ bÆ°áŧc phÃĒn tÃch mÃī hÃŽnh SEM
trÊn cÃģ Äáŧ tin cášy táŧt hay khÃīng thÃŽ bᚥn cᚧn phášĢi tháŧąc hiáŧn thÊm bÆ°áŧc kiáŧm Äáŧnh
Bootstrap nà y. CÃģ tháŧ nÃģi ÄÃĒy là bÆ°áŧc ÄÃĄnh giÃĄ Äáŧ tin cášy cáŧ§a cÃĄc Æ°áŧc lÆ°áŧĢng táŧŦ
mÃī hÃŽnh SEM.
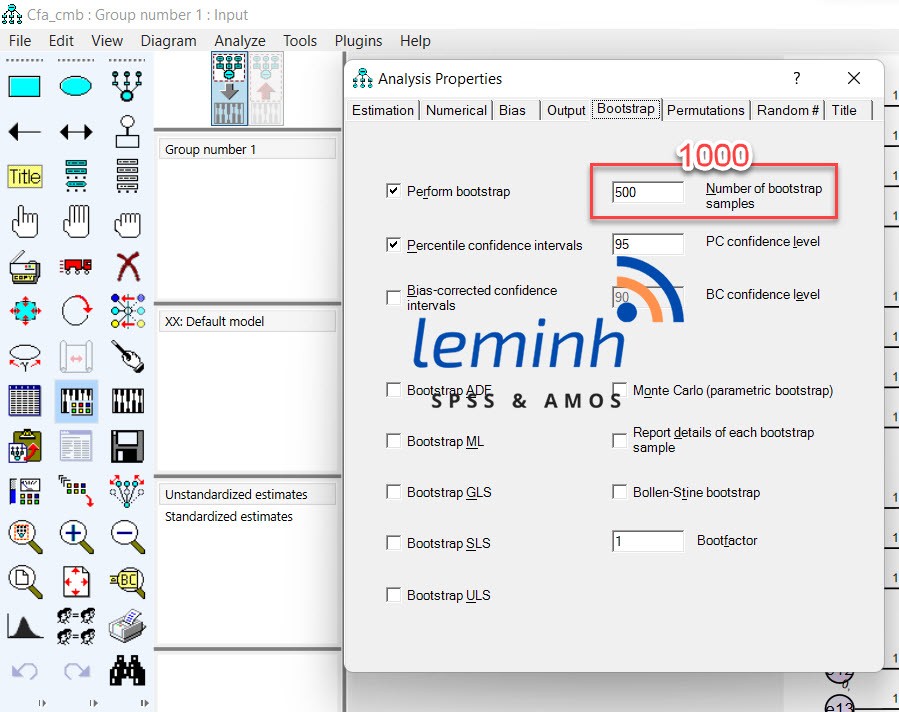
BÆ°áŧc Äᚧu tiÊn, trong mà n hÃŽnh SEM, bᚥn và o View/Analysis Properties/Bootstrap. TÃch và o Ãī Perform bootstrap và Äiáŧn sáŧ mášŦu bootstrap. ThÃīng thÆ°áŧng láŧąa cháŧn sáŧ lÆ°áŧĢng mášŦu bootstrap là khoášĢng 1000 nhÃĐ (theo Preacher, K. J., và Hayes, A. F., 2008), hÆĄn náŧŊa cÅĐng OK, nhÆ°ng mÃĄy chᚥy hÆĄi náš·ng, 1000 là Äáŧ§ Äáŧ phÃĐp tháŧ háŧi táŧĨ, láŧn hÆĄn cÅĐng ÄÆ°áŧĢc nhÆ°ng khÃīng cᚧn thiášŋt lášŊm. Giáŧ chÆ°ÆĄng trÃŽnh sáš― tᚥo ra 1000 mášŦu tháŧ, sau ÄÃģ phÃĒn tÃch SEM cho 1000 mášŦu nà y, và trášĢ váŧ giÃĄ tráŧ trung bÃŽnh cáŧ§a cÃĄc Æ°áŧc lÆ°áŧĢng trong máŧi mÃī hÃŽnh bootstrap.
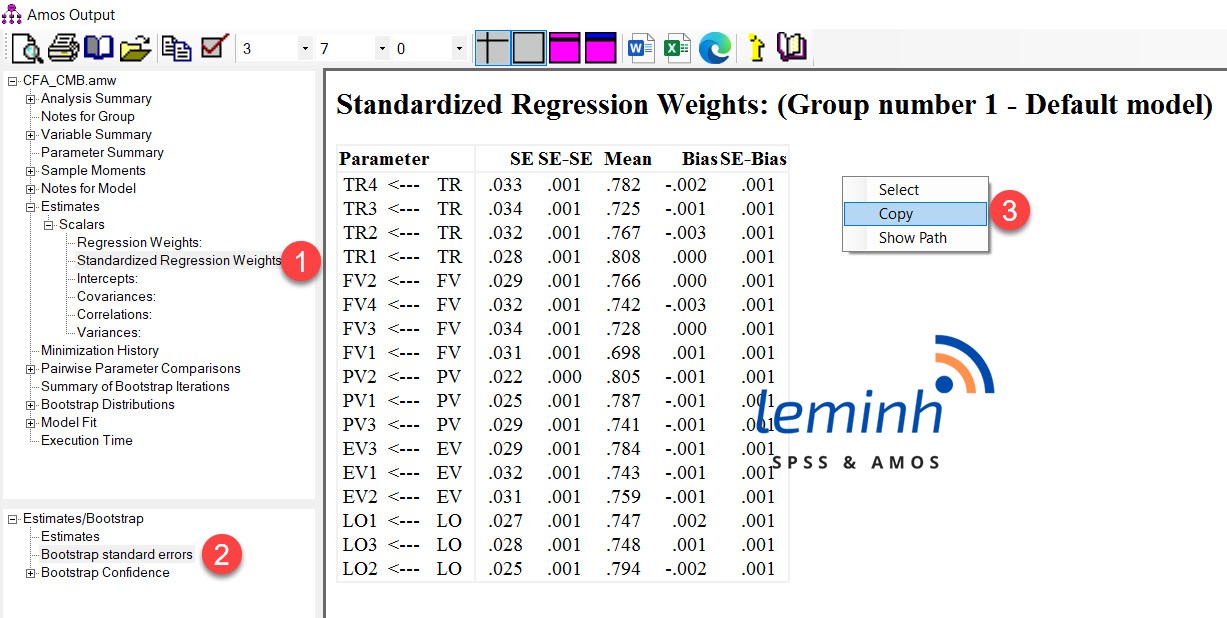
Cháŧn Viewtext Äáŧ xuášĨt hiáŧn háŧp thoᚥi Amos Output. NhášĨn cháŧn Standardized Regression Weights (1) và cháŧn tiášŋp Bootstrap standard errors (2). Click chuáŧt phášĢi cháŧn copy Äáŧ dÃĄn và o excel (3).
ChÚng ta tÃnh cháŧ sáŧ CR theo cÃīng tháŧĐc ÄÆ°áŧĢc tháŧ hiáŧn trong hÃŽnh bÊn dÆ°áŧi. CR < 1.96 thÃŽ cÃģ tháŧ kášŋt luášn kiáŧm Äáŧnh bootstrap Äᚥt yÊu cᚧu.
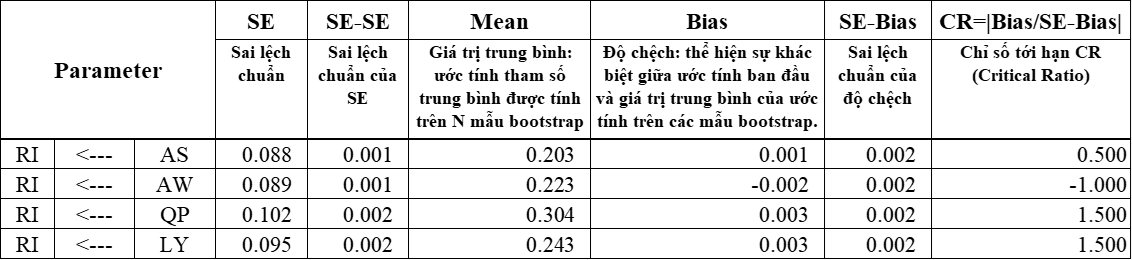
CÃĄc giÃĄ tráŧ |CR| < 1.96 nÊn kášŋt luášn Äáŧ cháŧch giáŧŊa 2 mášŦu (n - mášŦu thu thášp) và mášŦu (N - mášŦu láš·p lᚥi theo bootstrap) khÃĄc 0 khÃīng cÃģ Ã― nghÄĐa tháŧng kÊ. NÃģi cÃĄch khÃĄc, giáŧŊa mášŦu (n) và (N) khÃīng cÃģ sáŧą khÃĄc biáŧt. Do vášy kášŋt luášn rášąng, mášŦu (n) là ÄÃĄng tin cášy, cÃĄc Æ°áŧc lÆ°áŧĢng trong mÃī hÃŽnh SEM ÄÃĄng tin cášy.
GiÃĄ tráŧ ABS(CR) < 1.96 theo Äáŧ xuášĨt cáŧ§a Gao và cáŧng sáŧą (2008). NÄm 2013, Byrne xuášĨt bášĢn lᚧn tháŧĐ 2 cuáŧn sÃĄch Structural equation modeling with AMOS: Basic concepts, applications, and programming, Ãīng ÄÃĢ Äáŧ xuášĨt cháŧ sáŧ ABS(CR) âĪ 2; tuy nhiÊn trong lᚧn tÃĄi bášĢn tháŧĐ ba và o nÄm 2016, Byrne ÄÃĢ hiáŧu cháŧnh lᚥi cháŧ sáŧ ABS(CB) < 1.96.
Váŧ cÆĄ bášĢn khi kiáŧm Äáŧnh Äáŧ tin cášy cáŧ§a cÃĄc Æ°áŧc lÆ°áŧĢng thÃīng qua cháŧ sáŧ táŧi hᚥn CR cáŧ§a Bias trong nhiáŧu trÆ°áŧng háŧĢp rášĨt khÃģ Äᚥt báŧi nhiáŧu nguyÊn nhÃĒn khÃĄc nhau. NÊn thÃīng thÆ°áŧng, mÃŽnh thÆ°áŧng kášŋt luášn thÃīng qua tiÊu chà Äáŧ cháŧch (bias) nháŧ (âĪ 5â°). Và mÃŽnh cÅĐng rášĨt Ãt thášĨy bà i bÃĄo quáŧc tášŋ nà o Äáŧ cášp táŧi cháŧ sáŧ CR cáŧ§a Bias. Tuy nhiÊn, háŧ Äáŧ cášp táŧi Bootstrap bias-corrected confidence intervals áŧ máŧĐc Ã― nghÄĐa 10% (hay 5%) Äáŧ ÄÃĄnh giÃĄ cÃĄc máŧi quan háŧ trung gian mediation trong SEM (táŧĐc là kiáŧm tra xem máŧt biášŋn trung gian trong mÃī hÃŽnh nghiÊn cáŧĐu cÃģ phášĢi tháŧąc sáŧą ÄÃģng vai trÃē là biášŋn trung gian hay khÃīng, Äiáŧu nà y cÃģ Ã― nghÄĐa quan tráŧng trong vášĨn Äáŧ tÃŽm hiáŧu và ÄÆ°a ra hÆ°áŧng giášĢi quyášŋt cho táŧŦng vášĨn Äáŧ cáŧĨ tháŧ).
Tiášŋp theo, chÚng ta sáš― tÃŽm hiáŧu cÃĄch ÄÃĄnh giÃĄ biášŋn trung gian trong SEM nhÃĐ.
Äᚧu tiÊn, chÚng ta khai bÃĄo áŧ phᚧn bootstrap nhÆ° sau:
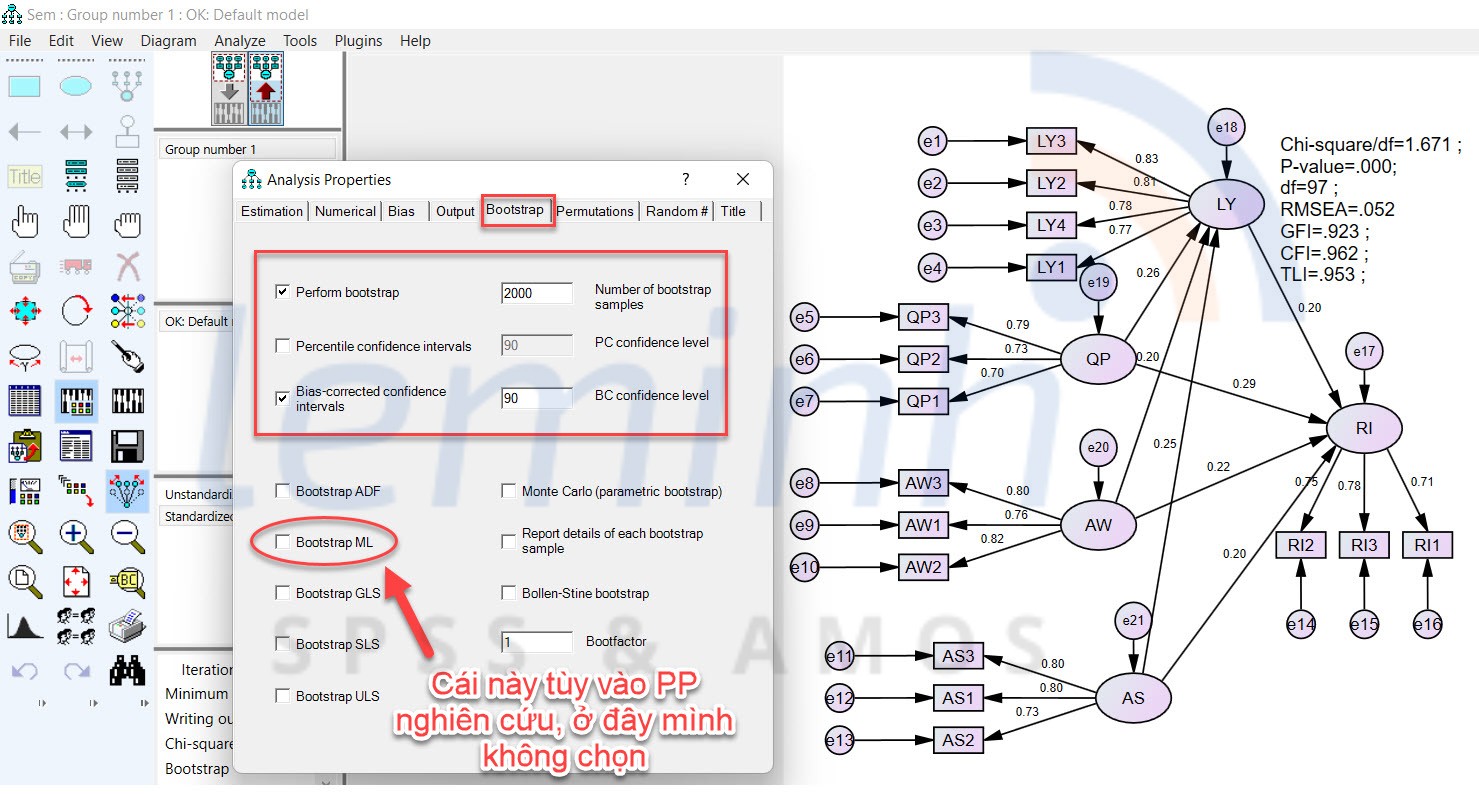
Sau ÄÃģ, chÚng ta cᚧn Äáŧnh nghÄĐa cÃĄc biášŋn giÃĄ tráŧ táŧng ášĢnh hÆ°áŧng giÃĄn tiášŋp trong mÃī hÃŽnh. BÆ°áŧc tháŧĐ nhášĨt là chÚng ta gÃĄn nhÃĢn cho tráŧng sáŧ háŧi qui cáŧ§a táŧŦng máŧi quan háŧ cᚧn xem xÃĐt nhÆ° hÃŽnh.
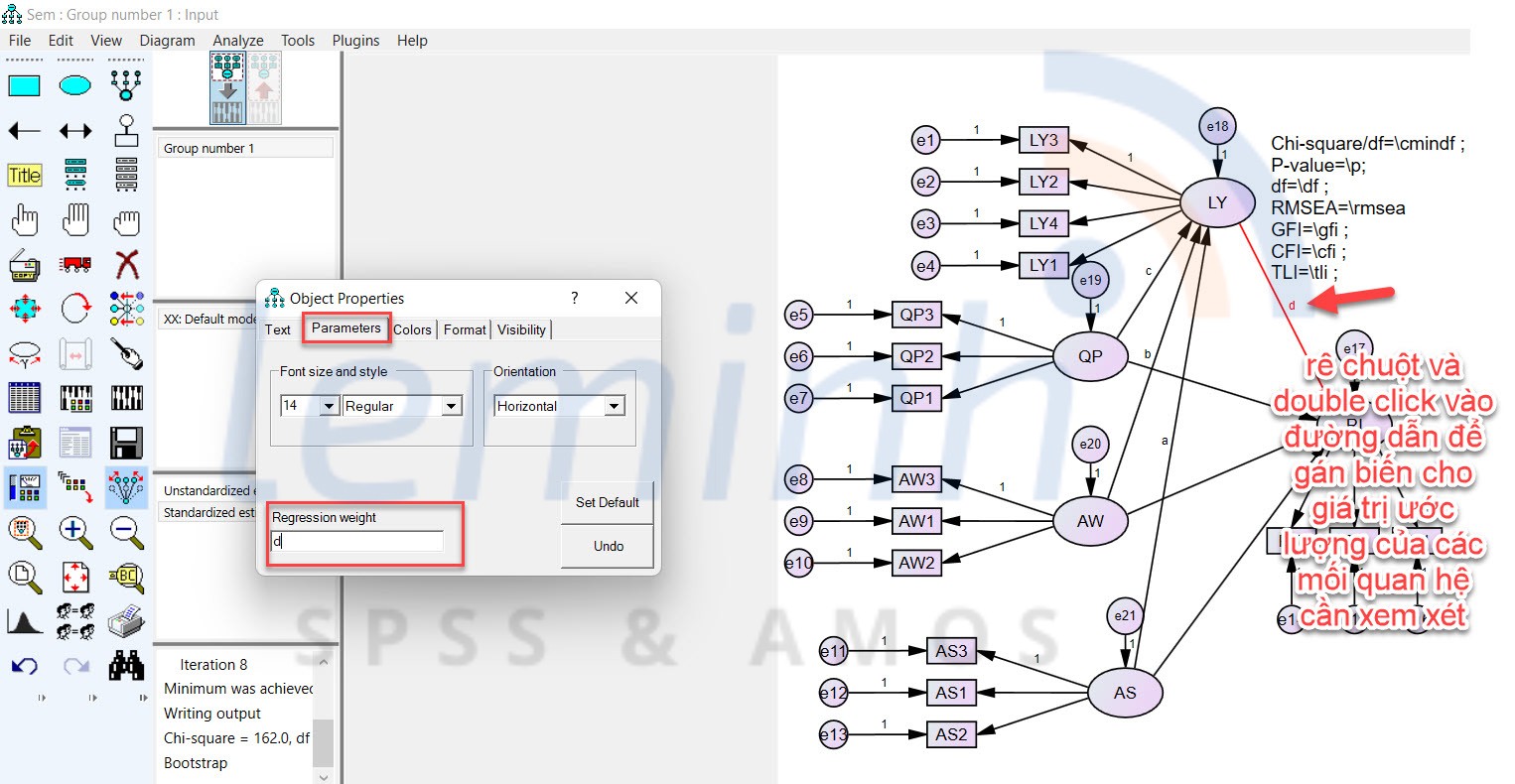
BÆ°áŧc hai, click chuáŧt trÃĄi và o dÃēng cháŧŊ Not estimating any user-defined estimand và nhášĨn cháŧn Define new estimands. Và viášŋt code tÆ°ÆĄng táŧą nhÆ° hÃŽnh dÆ°áŧi. Viáŧc xÃĄc Äáŧnh cÃīng tháŧĐc tÃnh giÃĄ tráŧ ášĢnh hÆ°áŧng giÃĄn tiášŋp trong mÃī hÃŽnh, chÚng ta nghiÊn cáŧĐu thÊm Kline (2016).
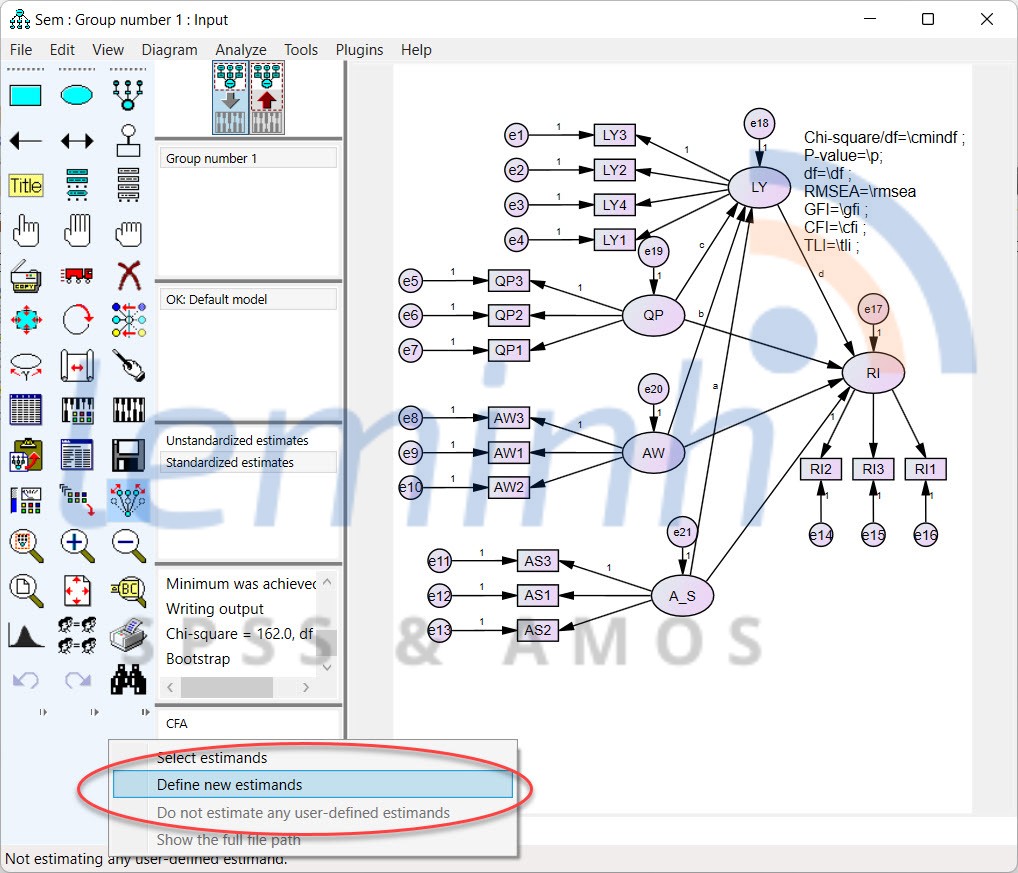
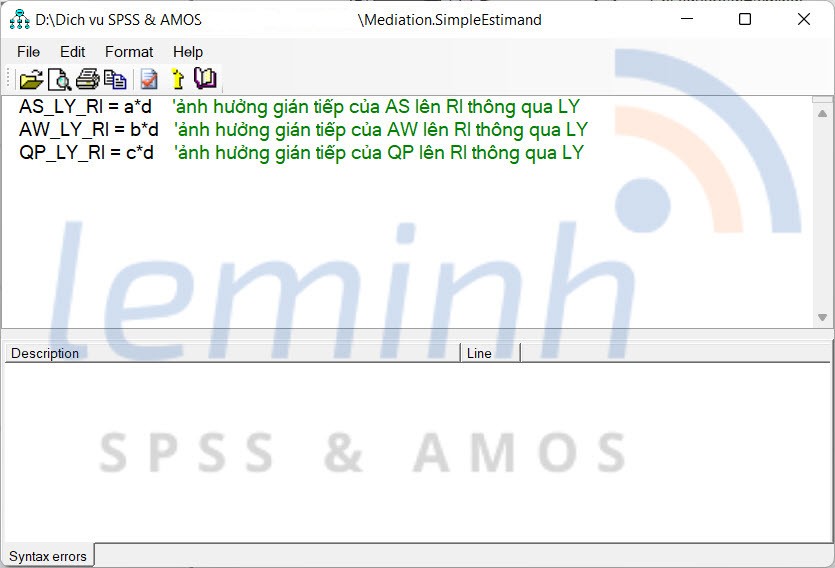
Sau khi viášŋt xong, chÚng ta lÆ°u váŧi tÊn bášĨt káŧģ và ÄÃģng lᚥi. TrÆ°áŧng háŧĢp cášĨu trÚc code báŧ láŧi, chÆ°ÆĄng trÃŽnh sáš― thÃīng bÃĄo láŧi áŧ phᚧn Syntax errors, và chÚng ta sáš― khášŊc pháŧĨc theo hÆ°áŧng dášŦn cáŧ§a háŧ nhÃĐ. Tiášŋp theo, chÚng ta chᚥy phÃĒn tÃch, và Äáŧc kášŋt quášĢ áŧ Output SEM. CÃģ máŧt Äiáŧu chÚng ta cᚧn lÆ°u Ã―, váŧi file code Æ°áŧc lÆ°áŧĢng Äáŧnh nghÄĐa sau máŧi lᚧn chᚥy phÃĒn tÃch thÃŽ AMOS sáš― khÃīng táŧą load, mà trášĢ váŧ dᚥng default, và do ÄÃģ ngÆ°áŧi dÃđng cᚧn load lᚥi áŧ lᚧn chᚥy tiášŋp theo. 
TrÆ°áŧng háŧĢp láŧi cášĨu trÚc thÃŽ chÆ°ÆĄng trÃŽnh sáš― hiáŧn thÃīng bÃĄo. LÚc nà y cᚧn click chuáŧt phášĢi và o dÃēng cháŧŊ Not estimating any user-defined estimand và nhášĨn cháŧn Edit mediation Äáŧ cháŧnh sáŧa.
CÚ phÃĄp cáŧ§a chÚng ta thÃŽ bÃŽnh thÆ°áŧng ráŧi, cÃģ Äiáŧu tÊn biášŋn AS trong SEM khÃīng ÄÆ°áŧĢc chášĨp nhášn, nÊn chÚng ta cᚧn chuyáŧn lᚥi tÊn A_S. Äáŧc kášŋt quášĢ.
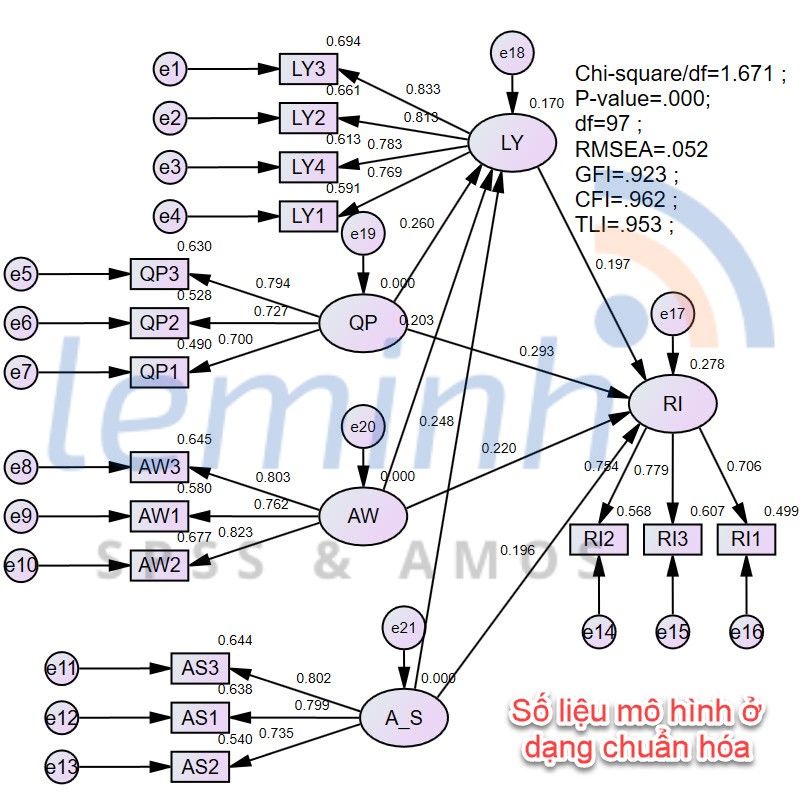
CÃĄc Æ°áŧc lÆ°áŧĢng mediation ÄÆ°áŧĢc Äáŧnh nghÄĐa báŧi ngÆ°áŧi dÃđng sáš― xuášĨt hiáŧn khi chÚng ta cháŧn User-defined estimands.
Dᚥng bášĢng kášŋt quášĢ thÆ°áŧng mÃŽnh trÃŽnh bà y nhÆ° sau, máŧi ngÆ°áŧi thÆ°áŧng hay háŧi nÊn sášĩn tiáŧn viášŋt ra ÄÃĒy luÃīn. LÆ°u Ã― trong cÃĄc nghiÊn cáŧĐu xuášĨt bášĢn áŧ Viáŧt Nam, chÚng ta nÊn Viáŧt hÃģa táŧŦ ngáŧŊ ra nhÃĐ.

GiÃĄ tráŧ p bootstrap âĪ 5% cÃģ nghÄĐa là táŧng cÃĄc tÃĄc Äáŧng giÃĄn tiášŋp cÃģ khÃĄc 0 ÄÃĄng káŧ áŧ bášĨt káŧģ máŧĐc Ã― nghÄĐa nà o. NÃģi cÃĄch khÃĄc, táŧn tᚥi quan háŧ trung gian cáŧ§a biášŋn LY trong mÃī hÃŽnh nghiÊn cáŧĐu.
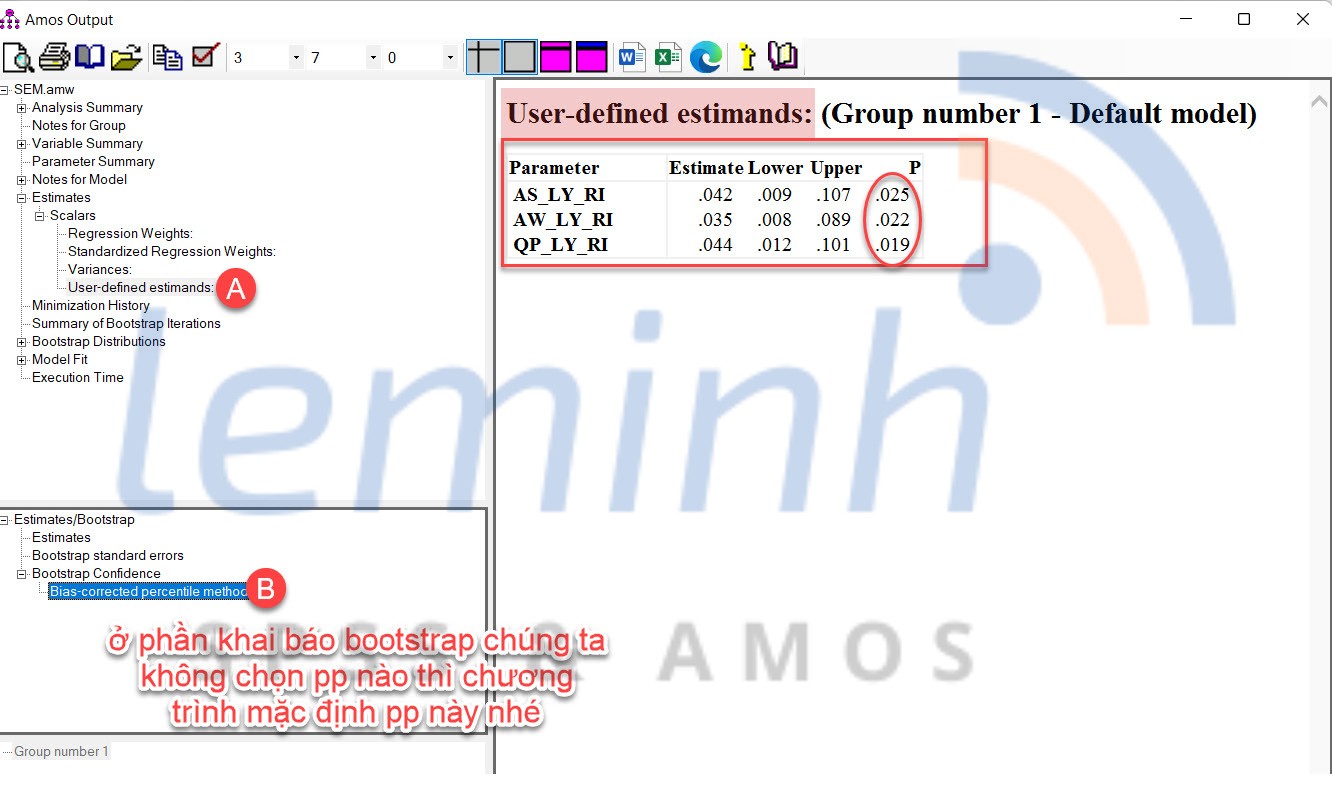
CÃģ máŧt Äiáŧu lÆ°u Ã― là cÃĄc giÃĄ tráŧ Æ°áŧc lÆ°áŧĢng thu ÄÆ°áŧĢc táŧŦ viáŧc code là giÃĄ tráŧ chÆ°a chuášĐn hÃģa, nhÆ°ng Äiáŧu nà y khÃīng quÃĄ quan tráŧng báŧi láš― chÚng ta cháŧ cᚧn kášŋt luášn cÃģ hay khÃīng táŧn tᚥi quan háŧ trung gian trong mÃī hÃŽnh nghiÊn cáŧĐu. Äáŧ ÄÃĄnh giÃĄ máŧĐc Äáŧ ášĢnh hÆ°áŧng cáŧ§a cÃĄc biášŋn Äáŧc lášp, bao gáŧm ášĢnh hÆ°áŧng tráŧąc tiášŋp và giÃĄn tiášŋp, chÚng ta cᚧn xem xÃĐt máŧĨc Matrices (Äáŧ xuášĨt hiáŧn máŧĨc nà y, trong phᚧn khai bÃĄo kášŋt quášĢ Output SEM trÆ°áŧc khi chᚥy chÚng ta nháŧ cháŧn  .
.
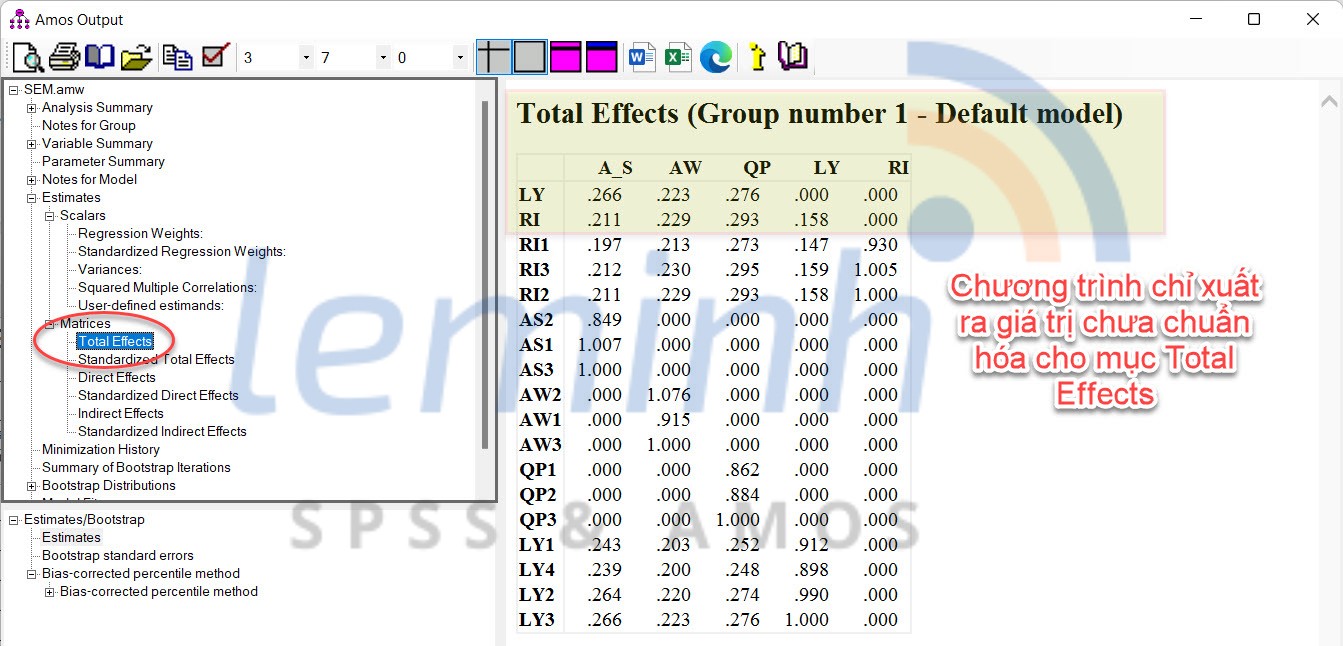
ChÚng ta cᚧn lÆ°u Ã―, cÃĄc giÃĄ tráŧ trong bášĢng Total Effects ÄÆ°áŧĢc chÆ°ÆĄng trÃŽnh máš·c Äáŧnh là chÆ°a chuášĐn hÃģa. Äáŧ tÃnh táŧng cÃĄc Æ°áŧc lÆ°áŧĢng chuášĐn hÃģa mÃŽnh cᚧn tháŧąc hiáŧn tÃnh toÃĄn tháŧ§ cÃīng theo cÃīng tháŧĐc cáŧ§a Kline (2016). CáŧĨ tháŧ trong bà i nà y chÚng ta tÃnh ÄÆ°áŧĢc nhÆ° sau.
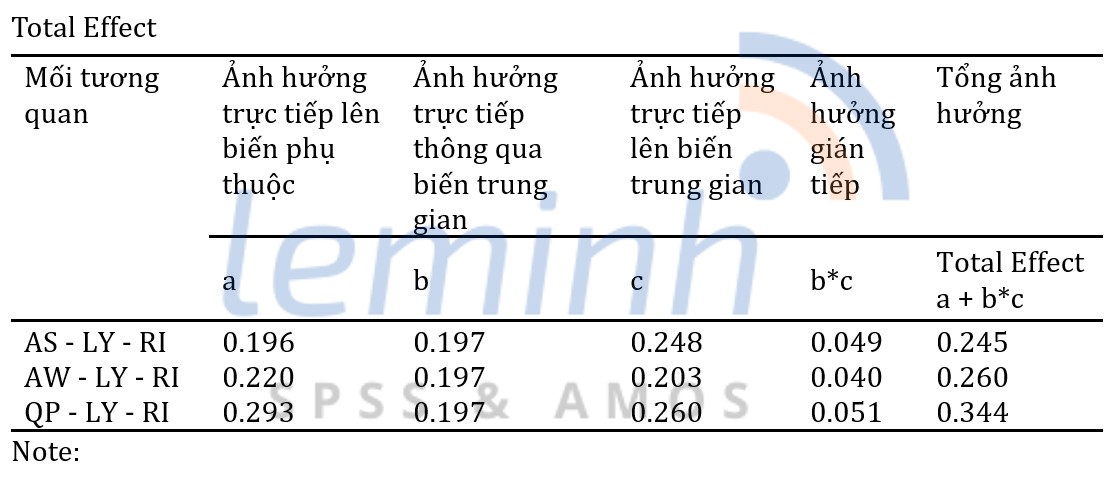
Cháŧ sáŧ T-statistics
Tiášŋp theo sau ÄÃĒy chÚng ta sáš― tÃnh toÃĄn cháŧ sáŧ tháŧng kÊ t-statistics. Äáŧ tÃnh toÃĄn ÄÆ°áŧĢc t-statistics chÚng ta cᚧn háŧ sáŧ beta và sai sáŧ chuášĐn. Äáŧ lášĨy háŧ sáŧ beta chÚng ta và o Estimates -> User-defined estimands và táŧŦ Estimates/Bootstrap chÚng ta cháŧn Bias-corrected percentile method. Äáŧ lášĨy sai sáŧ chuášĐn (SE) chÚng ta và o Estimates -> User-defined estimands và táŧŦ Estimates/Bootstrap chÚng ta cháŧn Bootstrap standard errors. Chia háŧ sáŧ beta cho sai sáŧ chuášĐn ta sáš― ÄÆ°áŧĢc giÃĄ tráŧ t-statistics (Collier, J. E., 2020).
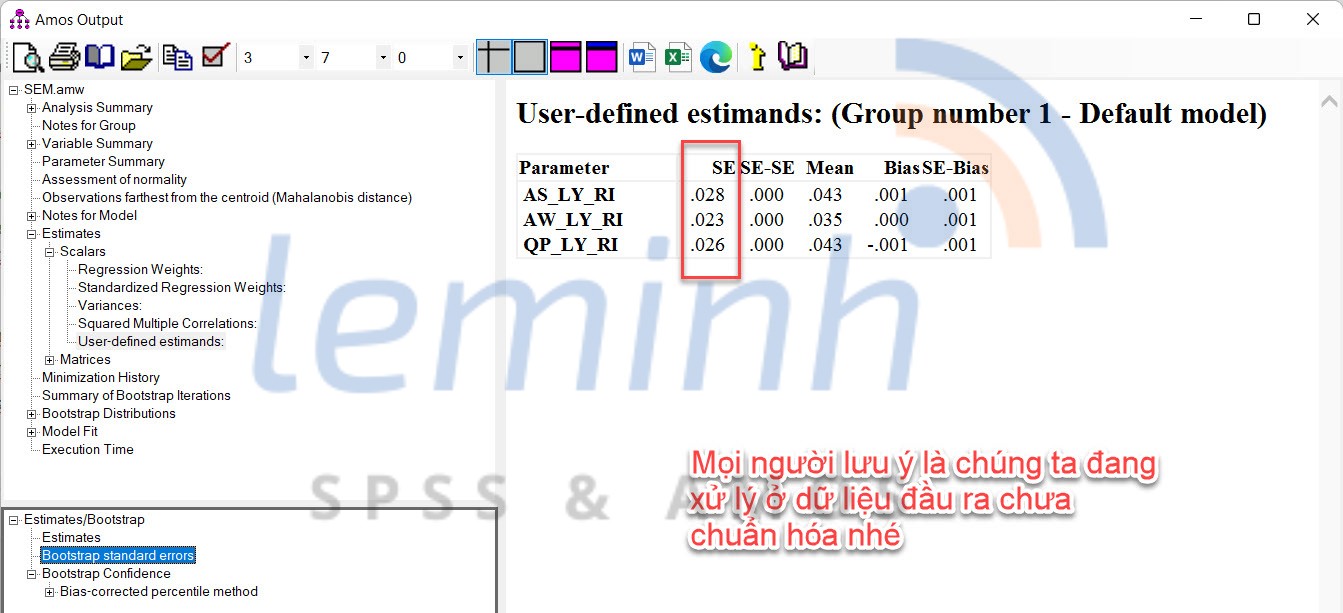
Váŧi AS-LY-RI: t-statistics là 0.042/0.028 = 1.500; AW-LY-RI: t-statistics là 0.035/0.023 = 1.522; QP-LY-RI: t-statistics là 0.044/0.026 = 1.692.
Kášŋt quášĢ phÃĒn tÃch mediation sáš― ÄÆ°áŧĢc trÃŽnh bà y lᚥi theo bášĢng sau.
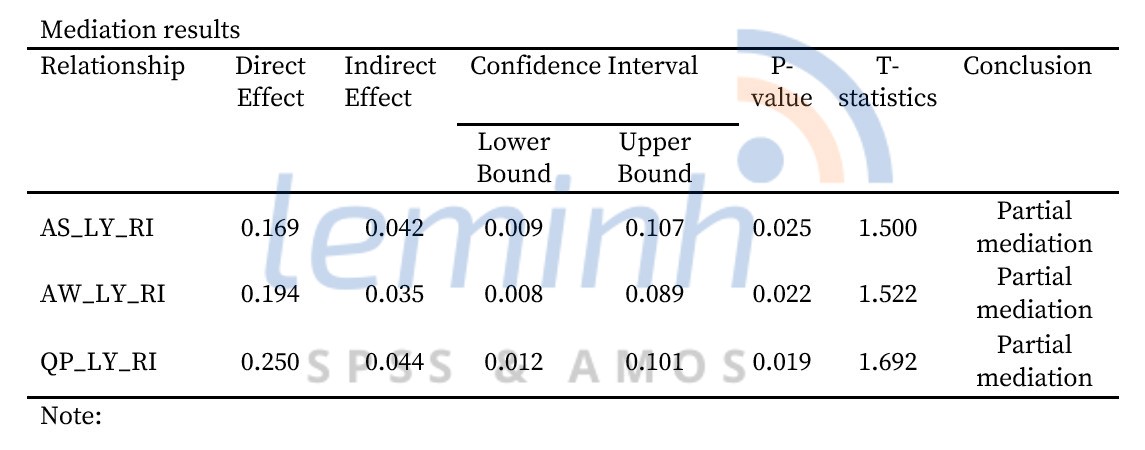
Cᚧn nÃģi thÊm máŧt tà áŧ phᚧn kášŋt luášn, khi ášĢnh hÆ°áŧng tráŧąc tiášŋp cÃģ hay khÃīng cÃģ Ã― nghÄĐa tháŧng kÊ (khÃīng quan tÃĒm) và ášĢnh hÆ°áŧng giÃĄn tiášŋp khÃīng cÃģ Ã― nghÄĐa tháŧng kÊ thÃŽ chÚng ta kášŋt luášn là No mediation. Khi ášĢnh hÆ°áŧng tráŧąc tiášŋp cÃģ Ã― nghÄĐa tháŧng kÊ và ášĢnh hÆ°áŧng giÃĄn tiášŋp cÃģ Ã― nghÄĐa tháŧng kÊ thÃŽ chÚng ta kášŋt luášn là Partial mediation. Và khi ášĢnh hÆ°áŧng tráŧąc tiášŋp khÃīng cÃģ Ã― nghÄĐa tháŧng kÊ và ášĢnh hÆ°áŧng giÃĄn tiášŋp cÃģ Ã― nghÄĐa tháŧng kÊ thÃŽ chÚng ta kášŋt luášn là Full mediation.

|
Máŧi
quan háŧ giÃĄn tiášŋp |
Máŧi
quan háŧ tráŧąc tiášŋp |
Kášŋt
luášn |
|
a*b cÃģ Ã― nghÄĐa
tháŧng kÊ (táŧĐc là cášĢ hai a và b Äáŧu cÃģ Ã― nghÄĐa tháŧng kÊ) |
câ cÃģ Ã― nghÄĐa tháŧng
kÊ |
Partial mediation |
|
a*b cÃģ Ã― nghÄĐa
tháŧng kÊ (táŧĐc là cášĢ hai a và b Äáŧu cÃģ Ã― nghÄĐa tháŧng kÊ) |
câ khÃīng cÃģ Ã―
nghÄĐa tháŧng kÊ |
Full mediation |
|
a*b khÃīng cÃģ Ã―
nghÄĐa tháŧng kÊ (táŧĐc là hoáš·c a hoáš·c b khÃīng cÃģ Ã― nghÄĐa tháŧng kÊ) |
KhÃīng quan tÃĒm Äášŋn
câ |
No mediation |
Äáŧ ÄÃĄnh giÃĄ váŧ máŧĐc Äáŧ ášĢnh hÆ°áŧng mᚥnh/trung bÃŽnh/yášŋu (mediating effect sizes) chÚng ta tham khášĢo tà i liáŧu cáŧ§a Cohen (1988; 2013): beta táŧŦ Âą0.1 Äášŋn Âą0.3 là nháŧ; beta táŧŦ Âą0.3 Äášŋn Âą0.5 là trung bÃŽnh; và beta táŧŦ Âą0.5 tráŧ lÊn là mᚥnh. GiÃĄ tráŧ beta (estimate) nášąm trong khoášĢng Âą1.
Äášŋn ÄÃĒy là chÚng ta ÄÃĢ hoà n thà nh phᚧn phÃĒn tÃch mediation cho mÃī hÃŽnh SEM. Máŧt vášĨn Äáŧ gáŧp Ã― nháŧ là chÚng ta cÅĐng khÃīng nÊn quÃĄ pháŧĐc tᚥp hÃģa vášĨn Äáŧ trong phÃĒn tÃch mediation, vášĨn Äáŧ nášąm áŧ giášĢi phÃĄp và kášŋt quášĢ Äᚥt ÄÆ°áŧĢc Äáŧ ÄÃĄp áŧĐng cÃĄc yÊu cᚧu cho máŧĨc tiÊu nghiÊn cáŧĐu.
TÃ i liáŧu tham khášĢo:
Amos Development Corporation, 2010. User-defined estimands.
http:// amosdevelopment.com /features/ userdefined/ userdefinedsimple/ Tutorial2/ pdf/ SimpleUserDefined2 .pdf. (Accessed 10 May 2021).
Byrne, B. M. (2013). Structural equation modeling
with AMOS: Basic concepts, applications, and programming. Routledge.
Byrne, B. M. (2016). Structural equation modeling with AMOS: Basic concepts, applications, and programming. Routledge.
Cohen, J. (1988). Statistical
power analysis for the behavioral sciences. Academic press.
Cohen, J., Cohen, P., West, S.
G., & Aiken, L. S. (2013). Applied multiple regression/correlation analysis
for the behavioral sciences. Routledge.
Collier, J. E. (2020). Applied structural equation modeling using AMOS: Basic to
advanced techniques. Routledge.
Kline, R. B. (2016). Principles and practice of
structural equation modeling. Guilford publications.
Preacher, K. J., & Hayes, A. F. (2008). âAssessing
mediation in communication researchâ. London:
The Sage sourcebook of advanced data analysis methods for communication
research.




